
The eccentric angle of the point where the line,
(A).
(B).
(C).
(D).
Answer
526.2k+ views
1 likes
Hint: As we know that the general equation of ellipse is
Complete step-by-step solution -
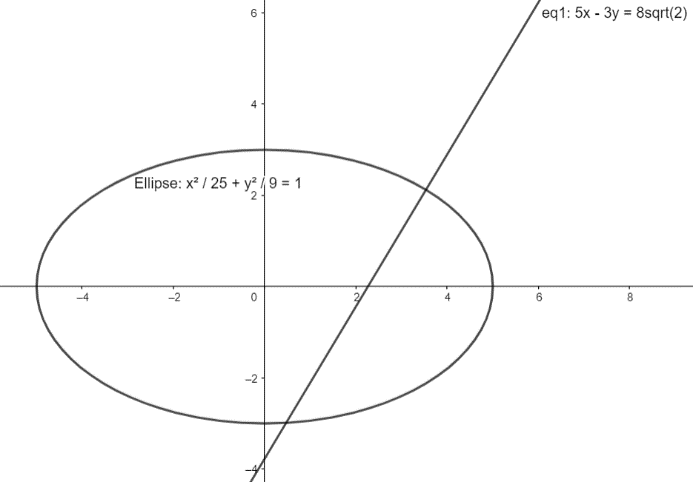
The general equation of the ellipse is at the point
According to the problem statement, we are given an ellipse equation as
By comparing it with the general equation, we get the length of the major axis, a = 5 and the length of minor axis, b = 3.
Putting the values of major and minor axis in equation
Also, the given normal equation in question:
Multiplying the equation (2) with
By comparing both the equation (1) and equation (3), the value of
We know that the value of
Hence, the eccentric angle of the point where the line,
Hence, option (b) is correct.
Note: The key steps involved in solving this problem is the conversion of given problem equations into standard form. By doing so, we can obtain the values of variables, and thus obtain the desired angle. The knowledge of trigonometric ratio at standard angles is also required to determine the final value.
Complete step-by-step solution -

The general equation of the ellipse is at the point
According to the problem statement, we are given an ellipse equation as
By comparing it with the general equation, we get the length of the major axis, a = 5 and the length of minor axis, b = 3.
Putting the values of major and minor axis in equation
Also, the given normal equation in question:
Multiplying the equation (2) with
By comparing both the equation (1) and equation (3), the value of
We know that the value of
Hence, the eccentric angle of the point where the line,
Hence, option (b) is correct.
Note: The key steps involved in solving this problem is the conversion of given problem equations into standard form. By doing so, we can obtain the values of variables, and thus obtain the desired angle. The knowledge of trigonometric ratio at standard angles is also required to determine the final value.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




