
The elastic limit of steel cable is $3.0 \times {10^8}N/{m^2}$ and the cross-section area is $4c{m^2}$. Find the maximum upward acceleration that can be given to a 900 kg elevator supported by the cable if the stress is not to exceed one-third of the elastic limit. If your answer is x, then mark the value of $\dfrac{x}{5}$.
Answer
571.2k+ views
Hint: The elastic limit is defined as the point of stress beyond which the material stops being elastic i.e. does not return to its original shape and size. That is the point where the material starts behaving like plastic. It is up to this point that the material obeys Hooke's law.
Complete step-by-step answer:
Let us understand the stress-strain curve,
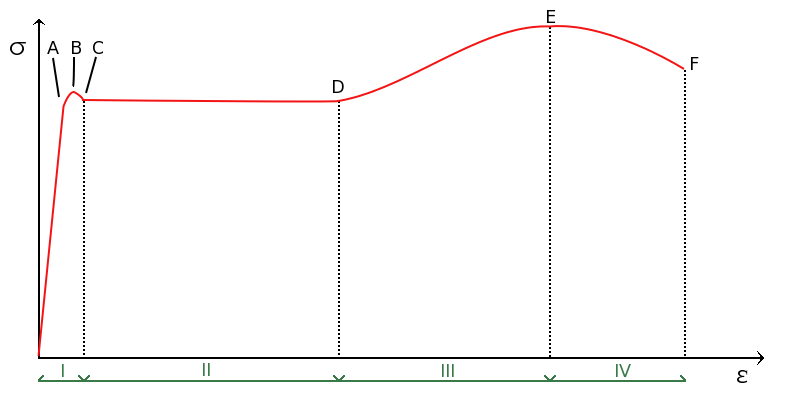
There are several critical points on the stress-strain curve which need to be understood. The first point A is called the elastic limit. This means that, up to the point A in the stress-strain curve, the stress-strain relation is linear in nature. This means that, up to this point, the material obeys Hooke’s Law.
Hooke’s Law:
$\sigma = E\varepsilon $ where $\sigma $is the stress, $\varepsilon $is the strain and the value $E$is called the Young’s Modulus, which is defined as the measure of stiffness of the solid body, the property which makes the solid return to its original shape and size after deforming it.
Elastic limit, $\sigma = \dfrac{F}{A}$ where F = force applied and A=area of cross-section.
Given,
$\sigma = 3.0 \times {10^8}N{m^{ - 2}}$
Since, they have asked to consider one-third the stress in the problem, $\sigma = \dfrac{{3.0 \times {{10}^8}}}{3} = {10^8}N{m^{ - 2}}$
$A = 4c{m^2}$
Substituting in the equation, we can obtain the force –
$
\sigma = \dfrac{F}{A} \\
F = \sigma A \\
F = {10^8} \times 4 \times {10^{ - 4}} \\
F = 4 \times {10^4}N \\
$
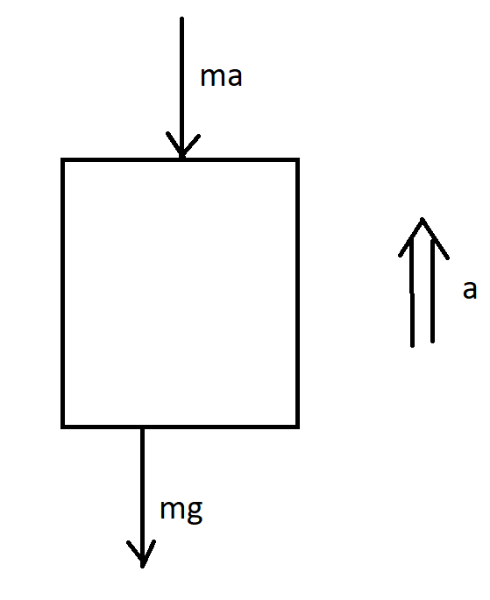
The force applied on the elevator due to acceleration, $F = W + ma$
where W=weight of the elevator, m=mass of the elevator
Given, mass $m = 900kg$
Therefore, the upward acceleration, $a = \dfrac{{F - W}}{m}$
$
a = \dfrac{{F - mg}}{m} \\
Substituting, \\
a = \dfrac{{4 \times {{10}^4} - 900 \times 9.81}}{{900}} \\
Solving, \\
a = \dfrac{{31171}}{{900}} = 34.64m{s^{ - 2}} \\
$
As per the given question, the acceleration to be taken = $\dfrac{a}{5} = \dfrac{{34.64}}{5} = 6.928m{s^{ - 2}}$
Therefore, the upward acceleration, $a = 6.928m{s^{ - 2}}$
Note: Students can often get confused while marking the direction of force for upward or downward acceleration. So, just remember the rule of thumb:
The force due to the acceleration $ma$ should be marked in the opposite direction to that of the acceleration.
Complete step-by-step answer:
Let us understand the stress-strain curve,

There are several critical points on the stress-strain curve which need to be understood. The first point A is called the elastic limit. This means that, up to the point A in the stress-strain curve, the stress-strain relation is linear in nature. This means that, up to this point, the material obeys Hooke’s Law.
Hooke’s Law:
$\sigma = E\varepsilon $ where $\sigma $is the stress, $\varepsilon $is the strain and the value $E$is called the Young’s Modulus, which is defined as the measure of stiffness of the solid body, the property which makes the solid return to its original shape and size after deforming it.
Elastic limit, $\sigma = \dfrac{F}{A}$ where F = force applied and A=area of cross-section.
Given,
$\sigma = 3.0 \times {10^8}N{m^{ - 2}}$
Since, they have asked to consider one-third the stress in the problem, $\sigma = \dfrac{{3.0 \times {{10}^8}}}{3} = {10^8}N{m^{ - 2}}$
$A = 4c{m^2}$
Substituting in the equation, we can obtain the force –
$
\sigma = \dfrac{F}{A} \\
F = \sigma A \\
F = {10^8} \times 4 \times {10^{ - 4}} \\
F = 4 \times {10^4}N \\
$

The force applied on the elevator due to acceleration, $F = W + ma$
where W=weight of the elevator, m=mass of the elevator
Given, mass $m = 900kg$
Therefore, the upward acceleration, $a = \dfrac{{F - W}}{m}$
$
a = \dfrac{{F - mg}}{m} \\
Substituting, \\
a = \dfrac{{4 \times {{10}^4} - 900 \times 9.81}}{{900}} \\
Solving, \\
a = \dfrac{{31171}}{{900}} = 34.64m{s^{ - 2}} \\
$
As per the given question, the acceleration to be taken = $\dfrac{a}{5} = \dfrac{{34.64}}{5} = 6.928m{s^{ - 2}}$
Therefore, the upward acceleration, $a = 6.928m{s^{ - 2}}$
Note: Students can often get confused while marking the direction of force for upward or downward acceleration. So, just remember the rule of thumb:
The force due to the acceleration $ma$ should be marked in the opposite direction to that of the acceleration.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

Which animal has three hearts class 11 biology CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




