Question

The electric field between the plates of two oppositely charged plane sheets of charge density$'\sigma '$is:

$A.\quad \dfrac{+\sigma }{2{{\in }_{0}}}$
$B.\quad \dfrac{-\sigma }{2{{\in }_{0}}}$
$C.\quad \dfrac{\sigma }{{{\in }_{0}}}$
$D.\quad Zero$

Answer 1

Hint: Knowledge of gauss law in electrostatics is necessary to solve this problem. Further, how the gauss law is used in different conditions, such as gauss law in the case of linear charge density, surface charge density and lastly in the case of volume charge density will be helpful too. The electric field for an infinite sheet of charge is given by, $E=\dfrac{\sigma }{2{{\in }_{0}}}$. The difference in the electric fields in between the plane sheets will give the solution.

Step by step solution:
Let’s start by finding out the electric field for a single plane infinitely charged sheet by making a diagram of it.

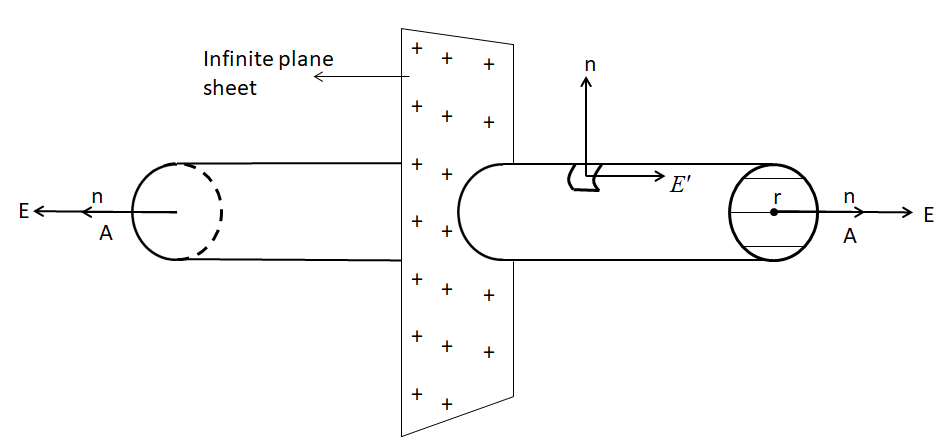
We have an infinitely large thin plane sheet having an uniform charge density $+\sigma $ throughout the surface. A charge is brought from infinity to a point at a distance r from the sheet. We will make a Gaussian surface as a cylinder of twice the same length from the sheet to the point passing through the sheet at the center of the cylinder.
 The cross sectional area of the cylinder will be A.

Now let’s find out the Flux $'\phi '$ through the cylinder.
We know from gauss law: $\phi =\int{E.dS}$

Here, we have three surface area components. The 2 cross sectional area components, at the 2 opposite ends and the curved surface area components.

${{\phi }_{total}}={{\phi }_{cross\sec tion-1}}+{{\phi }_{cross\sec tion-2}}+{{\phi }_{curvedsurface}}$
Since, both the Electric field component and the area components will have the direction of outward normal. Hence, ${{\phi }_{cross\sec tion-1}}=\int{E.dA}$and${{\phi }_{cross\sec tion-2}}=\int{(-E).d{A}'}=\int{(-E).(-dA})=\int{E.dA}$

That is, the flux coming out of both the cross sectional areas are equal. Hence, when we calculate the net flux, they will add up.
Therefore, the net flux coming out of the cylinder will be,

 ${{\phi }_{total}}=2EA\cos {{0}^{0}}+EA\cos {{90}^{0}}$
\[\Rightarrow {{\phi }_{total}}=2EA\]

We also know that flux is equal to the net charge contained in the Gaussian surface. That is,$\phi =\dfrac{{{Q}_{enclosed}}}{{{\in }_{0}}}$
Since, we already have$\sigma $surface charge density, hence, here the charge will be $\sigma .Area.$
Therefore, ${{\phi }_{total}}=\dfrac{{{Q}_{enclosed}}}{{{\in }_{0}}}\Rightarrow {{\phi }_{total}}=\dfrac{\sigma A}{{{\in }_{0}}}=2EA$
This implies the electric field due to a single plane sheet is, $E=\dfrac{\sigma }{2{{\in }_{0}}}$.
Let’s make a diagram of this problem, where one of the sheets has surface charge density $'+\sigma '$ and the other having charge density $'-\sigma '$.

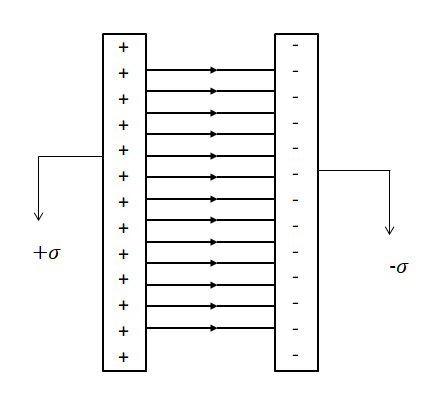
The Electric field due to the sheet having surface charge density of $'+\sigma '$ is, ${{E}_{1}}=\dfrac{\sigma }{2{{\in }_{0}}}$. Similarly, the electric field due to the sheet having surface charge density of $'-\sigma '$ is, \[{{E}_{2}}=\dfrac{-\sigma }{2{{\in }_{0}}}\].

The electric field between the two oppositely charged plane sheets of charge density$'\sigma '$is,$E={{E}_{1}}-{{E}_{2}}\Rightarrow E=\dfrac{\sigma }{2{{\in }_{0}}}-(\dfrac{-\sigma }{2{{\in }_{0}}})\Rightarrow E=\dfrac{\sigma }{{{\in }_{0}}}$.
Hence, the Electric field asked in the question is, $E=\dfrac{\sigma }{{{\in }_{0}}}$.

Note:
It is necessary to remember that, to find the net electric field due to the two infinitely charged plane sheets of charge having oppositely charged surface charge density is, $E={{E}_{1}}-{{E}_{2}}$ and not the other way around. This is because the electric field lines originate from a positively charged plate ${{E}_{1}}$ and moves towards the negatively charged plate ${{E}_{2}}$. Hence, $E={{E}_{1}}-{{E}_{2}}$ that is from the positively charged plate minus the negatively charged plate.