Question

The electrons are more likely to be found:

A. in the region a and b
B. only in region c
C. in the region a and c
D. only in the region a

Answer 1

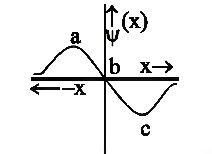
Hint:. The graph given in the question shows us the relation between $\psi $ and x. But, the probability depends on $P=4\pi {{x}^{2}}{{[\psi (x)]}^{2}}$. So, the graph needs to be converted to the respective square form and then we can find the required answer.

Complete step by step answer:
An atomic orbital is defined as the place inside an atom where the electron is likely to be present with a probability of 90% of the time. The probability of finding the electrons in a specified orbital depends on the wave function $\psi $. To be precise, the square of the wave function i.e ${{\psi }^{2}}$ can be used to find the electron density probability in a given orbital of an atom.
According to our graph, we have not been given the squares. However, we can still find the required probability by transforming the graph. We know that whenever a number is squared, be it a positive or negative integer, it is always positive (after squaring). Similarly, if the x-axis and y-axis of the graph, both are squared, then the negative parts flip themselves and become positive. That means, in perspective of y-axis, the region c gets inverted to the top and in perspective of x-axis, the region a gets flipped to the right.
In the final graph, we obtain 2 peaks, represented by the region a and c, where the probability of finding an electron is the maximum.
So, the correct answer is “Option C”.

Note: Generally, the 1s orbital has the maximum probability of finding an electron. In order to solve our question, we can simply mirror both the x-axis and y-axis and draw out our conclusion from the resultant graph. In case we had a negative peak in our final graph, that region would be the area where the probability of finding an electron is the least.