Question

What will be the equation of displacement in the following different conditions?

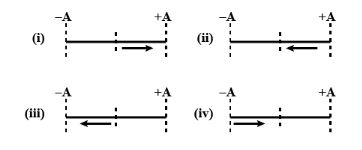
Answer 1

Hint: In the above diagrams we need to find the equation of displacement in given conditions. It is important to know about simple harmonic motion before starting the solution. The equation of Simple Harmonic Motion is (S.H.M) X=A Sin $\left( {\omega t + \phi } \right)$ here, X is the displacement and $\phi $ is the phase and A is the amplitude.

Complete step-by-step answer:
Step 1:
Before we start it is important to know about the Simple Harmonic Motion is (S.H.M).
Simple harmonic motion, in physics, repetitive movement back and forth through an equilibrium, or central, position, so that the maximum displacement on one side of this position is equal to the maximum displacement on the other side. The time interval of each complete vibration is the same. The force responsible for the motion is always directed toward the equilibrium position and is directly proportional to the distance from it. That is, F = −kx, where F is the force, x is the displacement, and k is a constant. This relation is called Hooke’s law
Consider a spring when a spring is at rest it has distance X(let). When the spring is disturbed then it starts oscillating and then it reaches to a position nearer to the attached point where X=-X and then again it releases with some restoring force to reach the original position. At X=0 it has the highest velocity.
Step 2:
Now, coming to the question. Consider (i) part
As told above the general eqn of S.H.M which is X=A Sin $\left( {\omega t + \phi } \right)$…….(1)

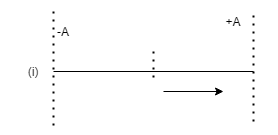
In this situation it is clearly visible that particle is at mean position and just started its oscillation, whenever a particle just starts its oscillation then it has no phase difference that means $\phi $ is zero
Putting this in eqn(1) we will get X=A Sin$\omega t$ .
Hence solved
Step 3:
Considering (ii) part

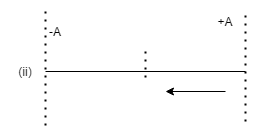
In the first case the particle starts from the rest and goes to the extreme position +A and now in part II it is returning from the extreme position, we can infer from this that the particle has a phase difference this time now.
The phase difference this time will be equal to $\pi $ because whenever a particle comes from the extreme position it has a phase difference equal to $\pi $ . Positive and negative signs depend on where it is coming.
Putting this in eqn (1) we will get X=A Sin $\left( {\omega t + \pi } \right)$
Step 4:
Considering (iii) part

This time from the origin to +A particle has covered A distance and then returned back to the mean position that means again a distance of A and now it is going to –A which is again at a distance of A from the mean position.
This time the phase distance will be equal to 3A and for this the phase difference will be equal to $\dfrac{{3\pi }}{2}$
Putting in eqn(1) we get X=A Sin$\left( {\omega t + \dfrac{{3\pi }}{2}} \right)$ .
Step 5:

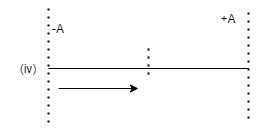
The particle returning from the extreme position of –A and phase will be $2\pi $
Putting in eqn(1) we get X=A Sin$\left( {\omega t + 2\pi } \right)$.

Additional Information: Below given are the few applications of SHM:
Clock.
Car Shock Absorbers.
Musical Instruments.
Bungee Jumping.
Diving Board.
The Process of Hearing.
Earthquake-proof buildings.
Metronome.

Note: In simple harmonic motion the curve travels a sine graph. It starts from the rest at zero position and then continues its oscillation until it has energy.
All the oscillations are simple harmonic motion but all the simple harmonic motion can’t be said as oscillatory motion.