Question

The equation of the director circle of the parabola ${y^2} = 16\left( {x - 1} \right)$ is
(A) ${x^2} + {y^2} = 3$
(B) ${x^2} + {y^2} = 1$
(C) $x - 3 = 0$
(D) $x + 3 = 0$

Answer 1

Hint: The director circle of a parabola is the directrix of the curve. The general form of the equation of a parabola is ${y^2} = 4ax$ , and the given equation of a parabola is ${y^2} = 16\left( {x - 1} \right)$ . Start with comparing both the equations and find the value of ‘a’. The general equation of directrix is $x + a = 0$ . Use this equation to represent the directrix for the given curve.

Complete step-by-step answer:
Here in this problem we are given an equation of a parabola ${y^2} = 16\left( {x - 1} \right)$ and using the properties of conic sections, we need to find the equation of the director circle of the given parabola.
Before starting to find the equation of the director circle, we must understand the director circle and the method to find it. In the conic section, the director circle of a curve is a circle consisting of all points where two perpendicular tangent lines to the curve cross each other. Since a parabola is not a closed curve, the director circle of a parabola is its directrix.
Parabolas are commonly known as the graphs of quadratic functions. They can also be viewed as the set of all points whose distance from a certain point (the focus) is equal to their distance from a certain line (the directrix).
There general form of the equation of a parabola is ${y^2} = 4ax$ , which has its focus on $\left( {a,0} \right)$ and vertex at $\left( {0,0} \right)$ . The equation for directrix for the general form of the equation can be given by $x + a = 0$
In the given parabola ${y^2} = 16\left( {x - 1} \right) = 4 \times 4\left( {x - 1} \right)$ , we have $a = 4$ and vertex at $\left( {1,0} \right)$

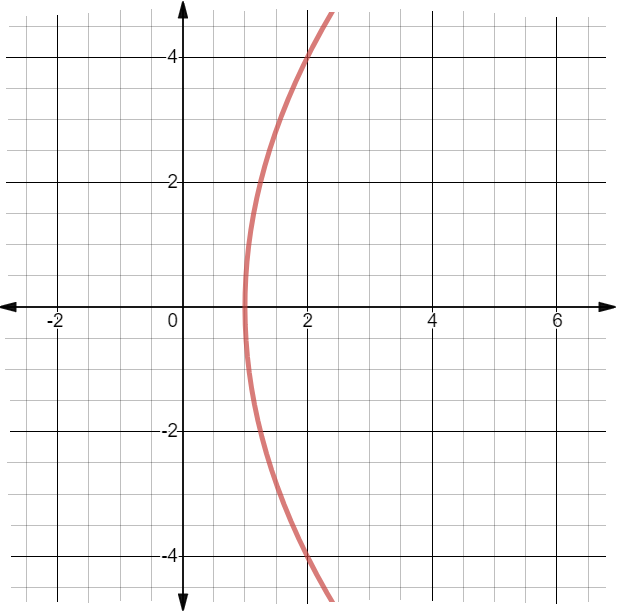
The focus of this given parabola is $\left( {a,0} \right) = \left( {4,0} \right)$
So the equation of directrix can be written by replacing $\left( {x - 1} \right)$ with $x$ and put $a = 4$ in the general equation of directrix.
$ \Rightarrow x + a = 0 \Rightarrow x - 1 + 4 = 0 \Rightarrow x + 3 = 0$
Therefore, we get an equation of the given parabola as $x + 3 = 0$ , which is an equation of a straight line passing through a point $\left( { - 3,0} \right)$ on the x-axis and parallel to the y-axis.
Hence, the option (D) is the correct answer.

Note: In the conic section, the use of the general form equation of curves and the related terms in general form always plays a crucial part in the solution. In this question, the question asked to find the equation of the director circle but instead, we got an equation of the directrix, which is a straight line. Here a straight line can be seen as a circle with a diameter equals to infinity. While for the curves like ellipse and hyperbola, the equation of the director circle is in the form of a circle, not a straight line.