Question

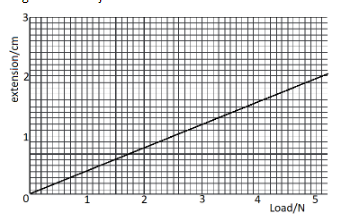
The extension/load graph for a spring is shown. The unstretched length of the spring is $ 15.0cm $ . When an object of unknown weight is suspended on the spring, the length of the spring is $ 16.4cm $ . What is the weight of the object?

(A) $ 0.55N $
(B) $ 0.67N $
(C) $ 3.5N $
(D) $ 4.1N $

Answer 1

Hint: From Hooke’s law, we can find the force as the product of the spring constant and the extension of the spring. Since the extension is given in the question, we can find the spring constant from the slope of the graph.

Formula used: In this solution, we will be using the following formula,
 $ F = kx $
where $ F $ is the force applied
 $ k $ is the spring constant and $ x $ is the distance that the spring is extended or compressed.

Complete step by step solution:
 In physics, Hooke's law states that the force that is needed to extend or compress a spring by a distance $ x $ is linearly proportional to this distance $ x $ .
Therefore, $ F \propto x $
So removing the constant of proportionality we get a constant $ k $
 $ \therefore F = kx $
This constant of proportionality is called the spring constant and is given by,
 $ k = \dfrac{F}{x} $
So in a graph between the force and the distance of extension or compression, the slope of the graph gives the value of $ k $ .
In the question, it is said that an object of unknown weight is suspended from the spring. This causes a downward force on the spring that causes the spring to extend.
In the question, we are given the graph of the extension versus the load and we can see it is a straight line.
Now since $ k = \dfrac{F}{x} $ so, the reciprocal of the slope of this graph will give us the spring constant.

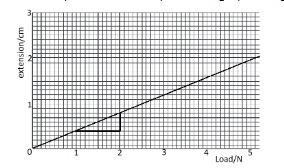
So we calculate the slope of the graph as,
Slope, $ m = \dfrac{{0.8 - 0.4}}{{2 - 1}} $
which gives us,
 $ m = \dfrac{{0.4}}{1} $
Therefore the spring constant is, $ k = \dfrac{1}{m} = \dfrac{1}{{0.4}} $
Now we need to calculate the extension of the spring.
In the question, it is given that the unstretched length of the spring is $ 15.0cm $ . And after the weight is suspended, the length of the spring becomes $ 16.4cm $ .
So the extended length is,
 $ x = \left( {16.4 - 15.0} \right)cm $
This gives us the value of extension as $ x = 1.4cm $
So now we can find the force, which is the weight of the body from the Hooke’s law as,
 $ F = kx = \dfrac{1}{{0.4}} \times 1.4 $
So we can remove the decimal points and get
 $ F = \dfrac{{14}}{4} $
On dividing, we get the weight of the body as,
 $ F = 3.5N $
So the correct answer is option C.

Note:
From Hooke’s law for springs it is often stated that the force $ F $ is the restoring force that is exerted by the spring on whatever is pulling on its other free end. In that case, the equation becomes,
 $ F = - kx $ , where the negative sign is present as the force is opposite to displacement.