Question

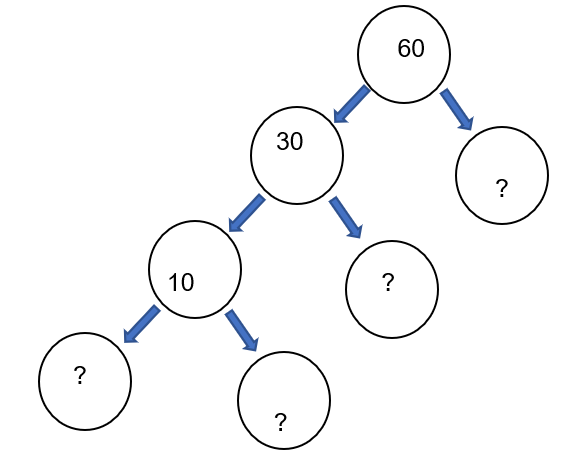
The factor tree for 60 is given. Write the missing numbers.

Answer 1

Hint: We try to process the factor tree and form the multiplication rule for the factors. From the one given factor we find the other one using division. The process continues for two more times. At the last process we break 10 into multiplication of two terms. Finally we form the factor free again to complete it.

Complete step by step answer:
The given image defines the factor tree. The primary term being 60. In every branching the main term x has been divided into two factors a and b in the multiplication form.
So, $x=a\times b$. This process continues for 3 times.
The starting value for x is 60. The one part of the breaking is 30. We need to find the other part. Let that be b. we consider 30 as a.
So, $60=30\times b$. This gives $b=\dfrac{60}{30}=2$. We got the first unknown as 2.
In the second breaking 30 has been broken into two parts, one being 10.
So, $x=30,a=10$. We get $30=10\times b$. This gives $b=\dfrac{30}{10}=3$. We got the second unknown as 3.
At the last breaking 10 has been broken in two parts out of which no term is given. So, we break the term 10 in factors. $10=1\times 10=2\times 5$.
So, we have two possible choices. We got the last two unknowns as $\left( 1,10 \right)$ or $\left( 2,5 \right)$. But if we take the first choice then the tree structure gets stuck. The primary value of 10 never changes. So, we take second choice of $\left( 2,5 \right)$.
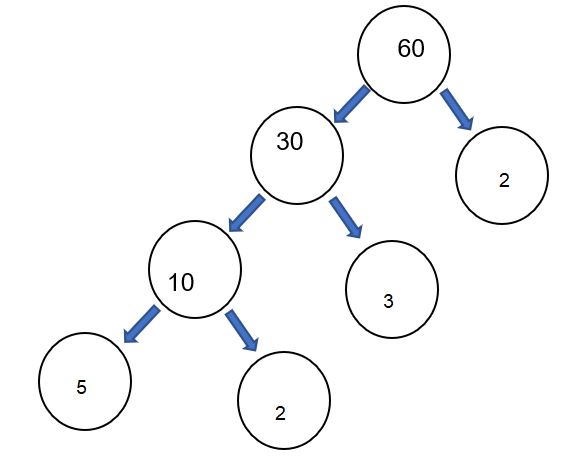
Now we create the diagram.

Note: We need to remember that when we are following the factor rule then there will always be a chance of breaking the primary part as the multiplication of that term itself and 1. The process gets stuck in recurring form in that process. We can’t allow that in a tree form.