Question

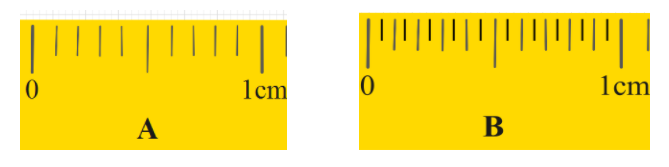
The figure below shows parts of measuring scales. Which scale can measure more accurately, $A$ or $B$?

Answer 1

Hint: We must know that accuracy is defined as the closeness of a measured value to a standard value. But In this case we will have to compare the least count of both scales. The scale with smaller least count would measure a quantity more accurately. It is like they are least count and accuracy in measurement are inversely related.

Complete step by step answer:
Firstly, we must have a clear idea about the least count of a measuring instrument. It is defined as the smallest measurement that can be taken by an instrument. The least count of any instrument can also be termed as the minimum change in measured quantity of the device which can be resolved on the scale of instruments.
Now, if we compare the least count of scale A and scale B. We can determine which scale can measure a quantity more accurately. Least count of these scale can be found using the formula,
 \[\text{L}\text{.C = }\dfrac{\text{smallest reading on main scale}}{\text{number of divisions}}\]
If we take scale A, the smallest reading on the main scale is $1cm$ and the number of divisions is 10. So the least count will be,
 \[\text{L}\text{.C =}\dfrac{1cm}{10}=1mm\]
Now, on scale B, it has the smallest reading as the same as scale A. But the number of divisions is 20. So, the least count will be,
\[\text{L}\text{.C =}\dfrac{1cm}{20}=0.5mm\]
So, the least count of scale B is smaller than that of scale A. therefore, scale B can measure more accurately.

Note: We can easily solve this question just by comparing the number of divisions. But we must understand the accuracy in this question refers to how closely either of the scales could measure a given quantity. Just by looking at the figure, we can understand that the number of divisions on scale B is more. So it will be having smaller least count and smaller least count means it could measure more precisely.