Answer
431.7k+ views
Hint: When Vernier scale is used for taking readings, we need to calculate the least count of Vernier and the number of divisions between each measurement. For calculating the value of$x$, we need to find the exact point where any of the markings on the Vernier scale coincides with one of the markings on the main scale.
Complete answer:
Calibration is expressed as the comparison of measurement values generated by a device under test with those of a calibration standard of known accuracy. A Vernier scale is basically a visual aid to take an accurate measurement reading between two graduation markings on a linear scale with the help of mechanical interpolation; thereby increasing the resolution and reducing the measurement uncertainty by using Vernier acuity to reduce possible errors.
The Vernier is a subsidiary measuring scale replacing a single measured-value pointer, and has a total of ten divisions equal in distance to nine divisions on the main scale. The interpolated reading is obtained by carefully observing which of the Vernier scale graduations is coinciding with a graduation on the main scale, which is easier to perceive than the visual estimation between two points. Such an arrangement of Vernier can go to higher resolution by using higher scale ratios, known as the Vernier constant. A Vernier scale can be used on circular or straight scales where a simple linear mechanism is adequate.
Let’s take an example to determine the reading through Vernier caliper:
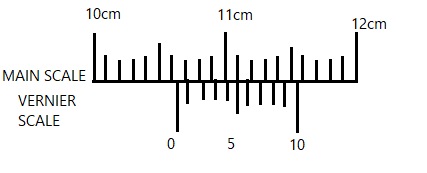
Main scale reading: $10\;cm$(Immediate left of zero)
Vernier scale reading:$0.02\;cm$(Alignment of scale lines)
Measurement reading:$10.02\;cm$
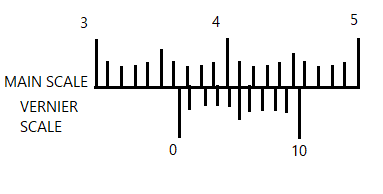
We are given a centimetre scale showing a particular position of Vernier scale. At the ${{5}^{th}}$reading of Vernier’s scale, both readings of the scales coincide. At the ${{4}^{th}}$reading of Vernier’s scale, the length between the two scales is minimum.
The last count of Vernier scale is $0.01\; cm$ So, the difference at ${{3}^{rd}}$reading of Vernier scale is, $2\times 0.01cm=0.002cm$
Difference at ${{2}^{nd}}$reading of Vernier scale is, $3\times 0.01=0.003cm$
Now,
Value of$x$is given as:
$x=0.3cm-3x\text{ scale division of vernier calliper}$
We get,
$x=0.3cm-3\times \dfrac{9}{100}cm$
$x=0.3cm-\dfrac{27}{100}cm$
$x=0.03cm$
The required value of$x$is $0.03\;cm$
Hence, the correct option is D.
Note:
In order to take the measurement readings from Vernier caliper properly, students need to remember the below points:
Consider that Vernier caliper output a measurement of$3.23\;cm$, this means that,
1. The main scale contributes the main number(s), and one decimal place to the reading. For example,$3.2\;cm$, whereby $3$ is the main number and $0.\;2$ is the one decimal place number.
2. The Vernier scale contributes the second decimal place to the measurement reading. For example, $0.03\;cm$.
Complete answer:
Calibration is expressed as the comparison of measurement values generated by a device under test with those of a calibration standard of known accuracy. A Vernier scale is basically a visual aid to take an accurate measurement reading between two graduation markings on a linear scale with the help of mechanical interpolation; thereby increasing the resolution and reducing the measurement uncertainty by using Vernier acuity to reduce possible errors.
The Vernier is a subsidiary measuring scale replacing a single measured-value pointer, and has a total of ten divisions equal in distance to nine divisions on the main scale. The interpolated reading is obtained by carefully observing which of the Vernier scale graduations is coinciding with a graduation on the main scale, which is easier to perceive than the visual estimation between two points. Such an arrangement of Vernier can go to higher resolution by using higher scale ratios, known as the Vernier constant. A Vernier scale can be used on circular or straight scales where a simple linear mechanism is adequate.
Let’s take an example to determine the reading through Vernier caliper:

Main scale reading: $10\;cm$(Immediate left of zero)
Vernier scale reading:$0.02\;cm$(Alignment of scale lines)
Measurement reading:$10.02\;cm$
We are given a centimetre scale showing a particular position of Vernier scale. At the ${{5}^{th}}$reading of Vernier’s scale, both readings of the scales coincide. At the ${{4}^{th}}$reading of Vernier’s scale, the length between the two scales is minimum.
The last count of Vernier scale is $0.01\; cm$ So, the difference at ${{3}^{rd}}$reading of Vernier scale is, $2\times 0.01cm=0.002cm$
Difference at ${{2}^{nd}}$reading of Vernier scale is, $3\times 0.01=0.003cm$
Now,
Value of$x$is given as:
$x=0.3cm-3x\text{ scale division of vernier calliper}$
We get,
$x=0.3cm-3\times \dfrac{9}{100}cm$
$x=0.3cm-\dfrac{27}{100}cm$
$x=0.03cm$
The required value of$x$is $0.03\;cm$
Hence, the correct option is D.
Note:
In order to take the measurement readings from Vernier caliper properly, students need to remember the below points:
Consider that Vernier caliper output a measurement of$3.23\;cm$, this means that,
1. The main scale contributes the main number(s), and one decimal place to the reading. For example,$3.2\;cm$, whereby $3$ is the main number and $0.\;2$ is the one decimal place number.
2. The Vernier scale contributes the second decimal place to the measurement reading. For example, $0.03\;cm$.
Recently Updated Pages
10 Examples of Evaporation in Daily Life with Explanations

10 Examples of Diffusion in Everyday Life

1 g of dry green algae absorb 47 times 10 3 moles of class 11 chemistry CBSE

What is the meaning of celestial class 10 social science CBSE

What causes groundwater depletion How can it be re class 10 chemistry CBSE

Under which different types can the following changes class 10 physics CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which are the Top 10 Largest Countries of the World?

How do you graph the function fx 4x class 9 maths CBSE

Who was the leader of the Bolshevik Party A Leon Trotsky class 9 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Which is the largest saltwater lake in India A Chilika class 8 social science CBSE

Ghatikas during the period of Satavahanas were aHospitals class 6 social science CBSE