Question

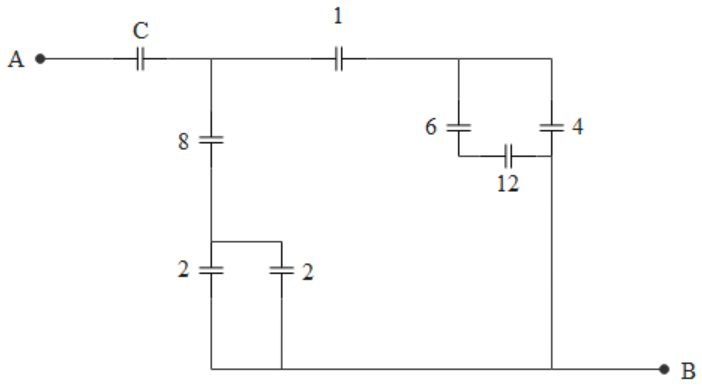
The figure shows a network of capacitors where the numbers indicate capacitances in micro Farad. The value of capacitance C such that the equivalent capacitance between point A and B is to be 1μF is:

A. $\dfrac{{32}}{{23}}\mu F$
B. $\dfrac{{31}}{{23}}\mu F$
C. $\dfrac{{33}}{{23}}\mu F$
D. $\dfrac{{34}}{{23}}\mu F$

Answer 1

Hint: Capacitor is a device which is used to store the charge. The charge stored in the capacitor depends on the potential difference applied across them and also depends on the capacitance of the capacitor. We have different formulas to find out effective capacitance when they are connected in series or parallel.
Formula used:
$\dfrac{1}{{{C_S}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}} + \dfrac{1}{{{C_4}}}{\text{ }}.........$
$ {C_P} = {C_1} + {C_2} + {C_3} + {C_4}{\text{ }}........... $

Complete step-by-step solution:
Generally, when there is more than one capacitor, we can connect them in series or we can connect them in parallel.
In the case of series connection, the current flowing through the circuit will be the same which means that the charge stored on every capacitor will be the same as the charge is nothing but the current flowing in a given time.
In the case of parallel connection, the voltage across all the capacitors will be the same.
In series connection charge will be the same and voltage will be divided across the capacitors whereas in parallel connection voltage will be the same and the charge will be divided across the capacitors.
Effective capacitance for capacitors in series connection is
$\dfrac{1}{{{C_S}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}} + \dfrac{1}{{{C_4}}}{\text{ }}.........$
Effective capacitance for capacitors in parallel connection is
${C_P} = {C_1} + {C_2} + {C_3} + {C_4}{\text{ }}...........$

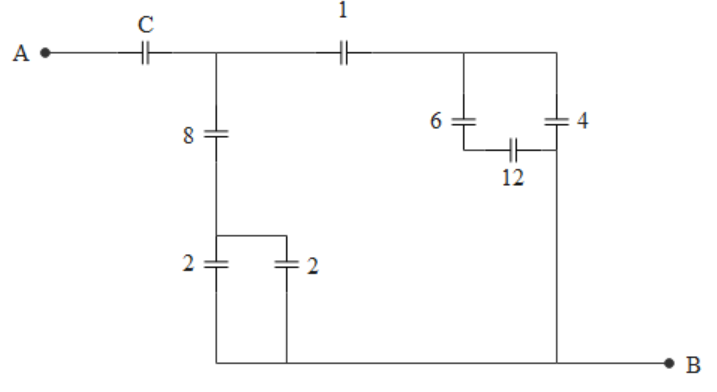
From the given circuit
12 and 6 are in series so effective capacitance will be
$\dfrac{1}{{{C_S}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}} + \dfrac{1}{{{C_4}}}{\text{ }}.........$
$\eqalign{
  & \Rightarrow \dfrac{1}{{{C_S}}} = \dfrac{1}{{12}} + \dfrac{1}{6} \cr
  & \Rightarrow {C_S} = \dfrac{{12 \times 6}}{{12 + 6}} \cr
  & \Rightarrow {C_S} = 4 \cr} $
Now this effective 4 and other 4 are in parallel. So the effective capacitance will be
${C_P} = {C_1} + {C_2} + {C_3} + {C_4}{\text{ }}...........$
$ \Rightarrow {C_P} = 4 + 4 = 8$
Now this 8 and 1 are in series. So the effective capacitance will be
$\eqalign{
  & {C_S} = \dfrac{{8 \times 1}}{{8 + 1}} \cr
  & \Rightarrow {C_S} = \dfrac{8}{9} \cr} $
Now 2 and 2 at the left bottom are parallel so the effective capacitance will be
${C_P} = 2 + 2 = 4$
This effective 4 is in series with 8. So the effective capacitance will be
$\eqalign{
  & {C_S} = \dfrac{{8 \times 4}}{{8 + 4}} \cr
  & \Rightarrow {C_S} = \dfrac{{32}}{{12}} \cr
  & \Rightarrow {C_S} = \dfrac{8}{3} \cr} $
Now finally this $\dfrac{8}{3}$ and $\dfrac{8}{9}$ are parallel. So the effective capacitance will be
${C_P} = \dfrac{8}{3} + \dfrac{8}{9} = \dfrac{{32}}{9}$
Finally this $\dfrac{{32}}{9}$ and capacitance C will be in series and the effective capacitance must be 1. So C will be
$\eqalign{
  & {C_S} = \dfrac{{\dfrac{{32}}{9} \times C}}{{\dfrac{{32}}{9} + C}} \cr
  & \Rightarrow 1 = \dfrac{{\dfrac{{32}}{9} \times C}}{{\dfrac{{32}}{9} + C}} \cr
  & \Rightarrow \dfrac{{32}}{9} + C = \dfrac{{32}}{9} \times C \cr
  & \Rightarrow C = \dfrac{{32}}{{23}}\mu F \cr} $
Hence option A will be the answer.

Note: The formulas which we have for the case of finding effective capacitance of parallel and series connection of capacitors will be exactly opposite to the case of finding effective resistance of parallel and series connection of resistors. If we know the voltage across AB we can find out the total charge passing through the system given as we had got the effective capacitance.