Question

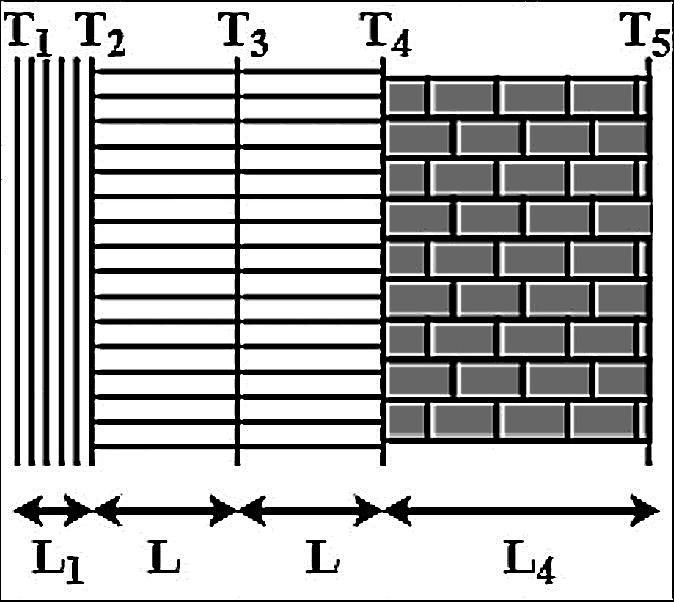
The figure shows the cross - section of the outer wall of a house built in a hill - resort to keep the house insulated from the freezing temperature of outside. The wall consists of teak wood of thickness ${L}_{1}$​ and brick of thickness ($L=5{ L }_{ 1 }$​). sandwiching two layers of an unknown material with identical thermal conductivities and thickness. The thermal conductivity of teak wood is ${K}_{1}$​ and that of brick is (${ K }_{ 4 }=5K$). Heat conduction through the wall has reached a steady state with the temperature of three surfaces being known. (${ T }_{ 1 }=25°C$, ${ T }_{ 2 }=20°C$ and ${ T }_{ 5 }=-20°C$). Find the interface temperature ${ T }_{ 4 }$​ and ${ T }_{ 3 }$​.

Answer 1

Hint: Use the formula for thermal resistance. Using the formula, find the thermal resistance of wood and brick walls. You will get resistance throughout to be the same. So, use the formula for thermal current. Equate the thermal current of each section. Substitute the given values and find the unknown interface temperatures i.e. ${ T }_{ 4 }$​ and ${ T }_{ 3 }$​.

Complete answer:

Let the area of interface be A.
Thermal Resistance is given by,
$R=\dfrac { L }{ KA }$
Thus, Thermal Resistance of wood is
${ R }_{ 1 }=\dfrac { { L }_{ 1 } }{ { K }_{ 1 }A }$ …(1)
And, thermal resistance of brick wall is
${ R }_{ 2 }=\dfrac { { L }_{ 4 } }{ { K }_{ 4 }A }$ …(2)
But, the thickness of brick is 5 times the thickness of wood and thermal conductivity of brick is 5 times the thermal conductivity of wood.
Thus, equation. (2) becomes,
${ R }_{ 2 }=\dfrac { { 5L }_{ 1 } }{ { 5K }_{ 1 }A }$
${ \Rightarrow R }_{ 2 }=\dfrac { { L }_{ 1 } }{ { K }_{ 1 }A }$ …(3)
From the equation. (1) and equation. (3),
${ R }_{ 1 }={ R }_{ 2 }$
Let the thermal resistance between each sandwich layer be R. As the resistance thought is same, thermal current through each wall is also the same.
$\Rightarrow \dfrac { 25-20 }{ { R }_{ 1 } } =\dfrac { 20-{ T }_{ 3 } }{ R } =\dfrac { { T }_{ 3 }-{ T }_{ 4 } }{ R } =\dfrac { { T }_{ 4 }+20 }{ { R }_{ 1 } }$
$\Rightarrow 25-20={ T }_{ 4 }+20$
$\Rightarrow { T }_{ 4 }=25-20-20$
$\Rightarrow { T }_{ 4 }=-15°C$ …(4)
Also, $ \dfrac { 20-{ T }_{ 3 } }{ R } =\dfrac { { T }_{ 3 }-{ T }_{ 4 } }{ R }$
$ \Rightarrow 20-{ T }_{ 3 }={ T }_{ 3 }-{ T }_{ 4 }$
$ \Rightarrow { T }_{ 3 }=\cfrac { 25+{ T }_{ 4 } }{ 2 }$ …(5)
Substituting equation. (4) in equation. (5) we get,
$ \Rightarrow { T }_{ 3 }=\cfrac { 20-15 }{ 2 }$
$ { T }_{ 3 }=2.5°C$
Hence, the interface temperature ${ T }_{ 4 }$​ and ${ T }_{ 3 }$ are​ $-15°C$ and $2.5°C$ respectively.

Note:
Thermal Conductivity denoted by K is the property of the material indicating its ability to conduct heat. Thermal conductivity is reciprocal of thermal resistivity. Heat transfer in materials of low thermal conductivity occurs at a lower rate as compared to the materials of high thermal conductivity. Thermal conductivity is an intrinsic property of the materials. It does not depend on the dimensions of the material. It depends on the temperature, density and moisture content of the material.