Question

The first angle of a triangle is one-third its second angle, where the third angle is 5 times the first angle. Find the measures of all the angles of the triangles.

Answer 1

Hint: We will start our solution by first writing down the property of triangle that states that the sum of all the internal angles of the triangle is ${{180}^{\circ }}$ , and then we will follow the conditions given in the question and write it in a form of common variable and then apply this property, in this way we will get the values of our angles.

Complete step by step answer:
Let the angles of the triangle be: ${{\theta }_{1}},{{\theta }_{2}}\text{ and }{{\theta }_{3}}$ .
Let ${{\theta }_{2}}$ be $x$ , then according to the information given in the question:
${{\theta }_{1}}=\dfrac{x}{3}$, and ${{\theta }_{3}}=5{{\theta }_{1}}\Rightarrow {{\theta }_{3}}=\dfrac{5x}{3}$

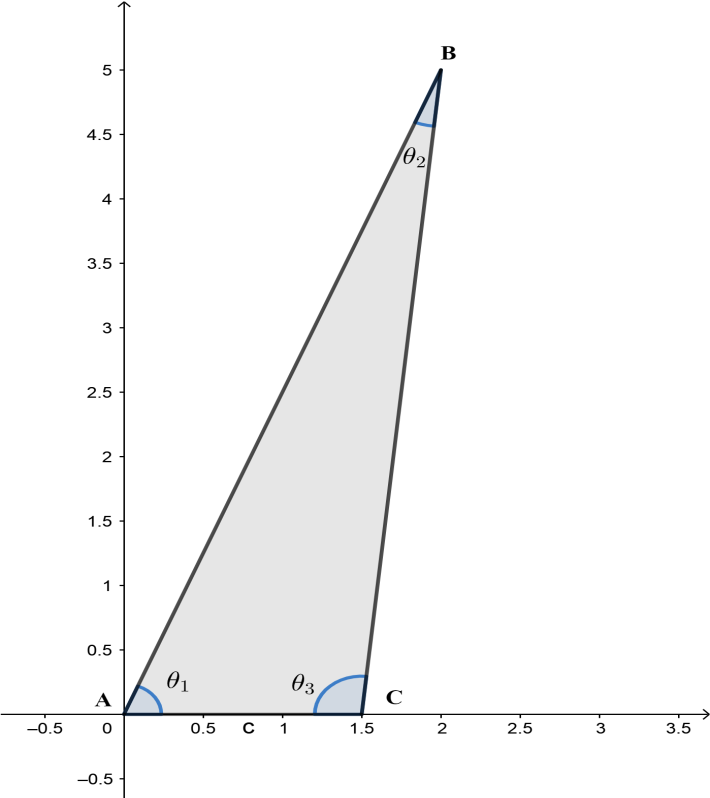
We know that according to the triangle’s property the sum of all the internal angles of the triangle is ${{180}^{\circ }}$.
Therefore in triangle ABC, we have${{\theta }_{1}}+{{\theta }_{2}}+{{\theta }_{3}}={{180}^{\circ }}$ .
Putting values of ${{\theta }_{1}},{{\theta }_{2}}\text{ and }{{\theta }_{3}}$ in this, then we will get: $\begin{align}
  & \left( \dfrac{x}{3} \right)+\left( x \right)+\left( \dfrac{5x}{3} \right)={{180}^{\circ }}\Rightarrow \dfrac{x+3x+5x}{3}={{180}^{\circ }} \\
 & \dfrac{9x}{3}={{180}^{\circ }}\Rightarrow x={{60}^{\circ }} \\
\end{align}$ .
Now we will use this value of x to find out value of all the angles:
$\begin{align}
  & {{\theta }_{1}}=\dfrac{x}{3}=\dfrac{60}{3}={{20}^{\circ }} \\
 & {{\theta }_{2}}=x={{60}^{\circ }} \\
 & {{\theta }_{3}}=\dfrac{5x}{3}=\dfrac{5\times 60}{3}={{100}^{\circ }} \\
\end{align}$

Therefore, the three angles of the triangles are: ${{20}^{\circ }},{{60}^{\circ }}\text{ and 10}{{\text{0}}^{\circ }}$

Note: Triangles are basically of three types on the basis of types of angles: Acute angle triangle (where all the angles are less than ${{90}^{\circ }}$), Right angle triangle (where at least one angle is ${{90}^{\circ }}$) and obtuse angle triangle ( where one angle is more than ${{90}^{\circ }}$ ), in all these triangle the sum of angle is ${{180}^{\circ }}$