Question

The foot of the perpendicular drawn from the origin on the line, $3x+y=\lambda \left( \lambda \ne 0 \right)$ is P. If the line meets the x-axis at A and y-axis at B, then the ratio BP: PA is
A. 9: 1
B. 1: 3
C. 1: 9
D. 3: 1

Answer 1

Hint: First draw the diagram according to the information mentioned in the question. Now, find the points A and B, find the slope by using the slope-intercept form. Use the condition of lines perpendicular to each other and find the slope of the line segment OP. Find the equation of line segment OP and use it to find point P. Finally use the section formula by internal division to find the ratio.

Complete step-by-step solution:
Let us first draw the x-axis and y-axis and plot the line and the other information according to the question.

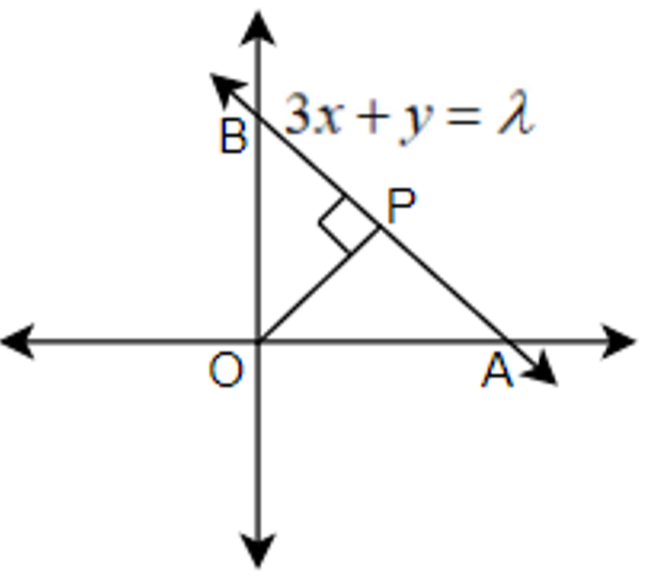
Here, we can see from the above diagram that the line cuts the x-axis at point A and cuts the y-axis at point B. Now, let us find the co-ordinates of point A and point B. For point A, we know that the y will be equal to zero. Hence, substituting, $y=0$ in the line equation $3x+y=\lambda $, we get,
$\begin{align}
  & 3x+0=\lambda \\
 & \Rightarrow 3x=\lambda \\
 & \Rightarrow x=\dfrac{\lambda }{3} \\
\end{align}$
Similarly, to find point B, we know that $x=0$, so we get,
$\begin{align}
  & 3\left( 0 \right)+y=\lambda \\
 & \Rightarrow 0+y=\lambda \\
 & \Rightarrow y=\lambda \\
\end{align}$
Hence, point $A=\left( \dfrac{\lambda }{3},0 \right)$ and point $B=\left( 0,\lambda \right)$. We know that the general slope-intercept form is, $y=mx+c$, where $m$ is the slope of the line, $c$ is the y-intercept. Let us convert the given line $3x+y=\lambda $ into $y=mx+c$ form. So, we get,
$y=-3x+\lambda $
Therefore, ${{m}_{AB}}=-3$. Since, the line AB and segment OP are perpendicular to each other, we can say that,
${{m}_{OP}}\times {{m}_{AB}}=-1$
We have, ${{m}_{AB}}=-3$, so let us find the value of ${{m}_{OP}}$.
$\begin{align}
  & {{m}_{OP}}\times \left( -3 \right)=-1 \\
 & \Rightarrow {{m}_{OP}}=\dfrac{1}{3} \\
\end{align}$
Now, we know the point-slope form $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$. Let us use this expression and find the equation of segment OP. We have segment OP passing through the origin, which is $O\left( 0,0 \right)=\left( {{x}_{1}},{{y}_{1}} \right)$ and ${{m}_{OP}}=\dfrac{1}{3}$. So,
$\begin{align}
  & y-0=\dfrac{1}{3}\left( x-0 \right) \\
 & \Rightarrow y=\dfrac{1}{3}x \\
 & \Rightarrow 3y=x \\
 & \Rightarrow x-3y=0 \\
\end{align}$
We have the equations of line AB and line segment OP as $3x+y=\lambda $ and $x-3y=0$ respectively. Now, let us substitute $x=3y$ in the line AB equation, so we get,
$\begin{align}
  & 3\left( 3y \right)+y=\lambda \\
 & \Rightarrow 9y+y=\lambda \\
 & \Rightarrow 10y=\lambda \\
 & \Rightarrow y=\dfrac{\lambda }{10} \\
\end{align}$
Substituting $y=\dfrac{\lambda }{10}$ in the line equation $x-3y=0$, we get,
$\begin{align}
  & x-3\left( \dfrac{\lambda }{10} \right)=0 \\
 & \Rightarrow x-\dfrac{3\lambda }{10}=0 \\
 & \Rightarrow x=\dfrac{3\lambda }{10} \\
\end{align}$
Therefore, the point P will be $\left( \dfrac{3\lambda }{10},\dfrac{\lambda }{10} \right)$. Now, let us suppose that P divides AB into $m:n$, so we get, $\dfrac{PA}{BP}=\dfrac{m}{n}$ . Therefore, by section formula of internal division, we have,
$x=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},y=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}$
We have $P\left( x,y \right)=\left( \dfrac{3\lambda }{10},\dfrac{\lambda }{10} \right),A\left( {{x}_{1}},{{y}_{1}} \right)=\left( \dfrac{\lambda }{3},0 \right),B\left( {{x}_{2}},{{y}_{2}} \right)=\left( 0,\lambda \right)$. Let us substitute these values in the expression of section formula. Let us substitute the value in $x=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n}$, so we get,
$\begin{align}
  & \dfrac{3\lambda }{10}=\dfrac{m\times \left( 0 \right)+n\times \dfrac{\lambda }{3}}{m+n} \\
 & \Rightarrow \dfrac{3\lambda }{10}=\dfrac{\dfrac{n\lambda }{3}}{m+n} \\
 & \Rightarrow 3\lambda \left( m+n \right)=10\times \dfrac{n\lambda }{3} \\
 & \Rightarrow 3m+3n=\dfrac{10n}{3} \\
 & \Rightarrow 3m=\dfrac{10n}{3}-3n \\
 & \Rightarrow 3m=\dfrac{10n-9n}{3} \\
 & \Rightarrow 3m=\dfrac{n}{3} \\
 & \Rightarrow \dfrac{m}{n}=\dfrac{1}{9} \\
\end{align}$
We have, $\dfrac{PA}{BP}=\dfrac{m}{n}=\dfrac{1}{9}$ , but we need, $\dfrac{BP}{PA}=\dfrac{n}{m}=\dfrac{9}{1}$ .
Therefore, BP: PA is 9: 1.
Hence, the correct answer is option A.

Note: In this question, the construction of the diagram according to the conditions mentioned makes it an important step, the next important step is to find the coordinates of the points A, B, and the point P which will be used for finding the ratio. You can also use the formula of y-coordinate of the point P and its corresponding section formula, $y=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}$ to find the required ratio.