Question

The force of buoyancy exerted by the atmosphere on a balloon is b in the upward direction and remains constant. The force of air resistance on the balloon acts opposite to the direction of velocity and is proportional to it. The balloon carries a mass M and is found to fall down near the earth's surface with a constant velocity v. How much mass should be removed from the balloon so that it may rise with a constant velocity v?

Answer 1

Hint:To solve this particular problem we have to first visualize the situation. There are different forces in action over the balloon. It is advised to draw each case which will give us a better perception of the solution to this problem.

Complete step by step answer:
Let M be the mass of the balloon.
Let the air resistance force on the balloon be F.
Given that the force of air resistance is proportional to the velocity, so we can write,
$F \propto v$ .
This can be rewritten as,
$F = kv$,
where k = proportionality constant.

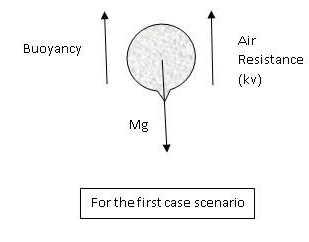
Now, considering the first scenario where the balloon is moving towards the ground at a constant velocity v, we can see from the figure that three forces are working on the balloon. Force of gravity (Mg), Buoyancy(B), and Air resistance (kv). As the balloon is falling at a constant velocity, all these three velocities must cancel each other thus considering the direction of the force we can write,
$B + kv = Mg$ .
This can be rewritten as,
$M = \dfrac{{B + kv}}{g}$.

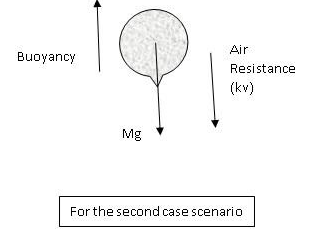
Now, in the second scenario where due to the reduction in mass the balloon starts rising at a constant velocity v. In this case let the Mass be $M'$.
In this case also as the balloon is rising at a constant velocity, all these three velocities must cancel each other thus considering the direction of the force we can write,
$B = M'g + kv$ .
This equation can be rewritten as,
$M' = \dfrac{{B - kv}}{g}$
Thus, the amount of mass to be removed for the balloon to rise can be given as,
$\Delta M = M - M'$
Putting the values of M and $M'$from the above equations we get,
$\Delta M = \dfrac{{B + kv}}{g} - \dfrac{{B - kv}}{g}$
Solving this equation, we get,
$\Delta M = \dfrac{{B + kv - B + kv}}{g} = \dfrac{{2kv}}{g}$. ----(1)
Again, from the first scenario we get,
$B + kv = Mg$,
This can be also written as $kv = Mg - B$ .
Putting this value in (1) we get,
$\Delta M = \dfrac{{2(Mg - B)}}{g} = 2(M - \dfrac{B}{g})$ .
Thus, to make the balloon move in an upward direction with a constant velocity v, we have to reduce a mass of $\dfrac{B}{g}$.

Note:This is a very conceptual question so it has to be solved very nicely using all the necessary diagrams/ figures. It is suggested for all students to draw figures to calculate for this kind of problem as it is very easy to make an error in this kind of question.