Question

The force required to just move a body up the inclined plane is double the force required to just prevent the body from sliding down the plane. The coefficient of friction is $\mu$. The inclination $\theta$ of the plane is:
$A. \tan ^{ -1 }{ \mu }$
$B. \tan ^{ -1 }{ \dfrac { \mu }{ 2 } }$
$C. \tan ^{ -1 }{ 2\mu }$
$D. \tan ^{ -1 }{ 3\mu }$

Answer 1

Hint: Making the free body diagram will help you to understand how the forces are acting on the body in each case. The first case is when the force acts on the body, when the body is just about to move up. In this case, the frictional force acts against the direction of force acting on the body.
The second case is when the force acts on the body to prevent it from slipping. In this case, the frictional force acts along the direction of the force acting on the body.
Then we just need to equate the horizontal force and vertical force for both the equations. On solving those equations, we will get the value of inclination.

Complete step-by-step answer:
Now we make the basic force body diagrams for 2 cases. The explanation of the cases will be discussed below; we first understand the forces involved and how to make the force body diagram.
The inclination is considered $\theta$ and we have the body on the inclined plane. Drawing perpendiculars to it from the center of mass of the body will give us the force due to gravity acting vertically downward. The sine and cosine components of this force and the Normal component of this force are upon the other perpendiculars as per the diagram.
We know that the frictional force${ f }_{ \mu }$ is given by ${ f }_{ \mu }=\mu N$.
$N=mg\cos { \theta }$
Now, let’s understand the 2 cases:

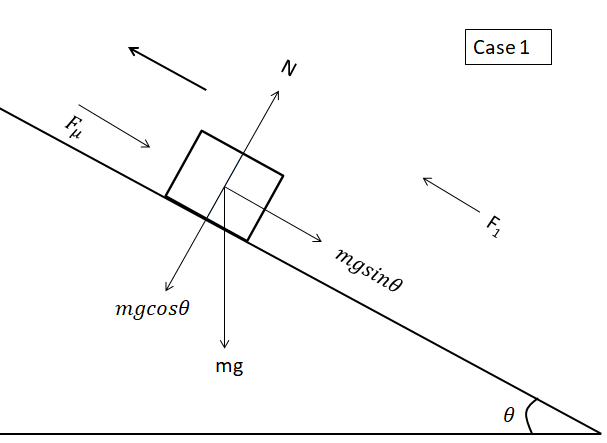
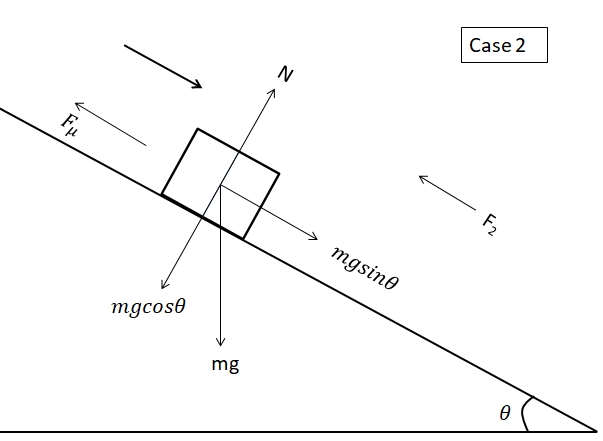
Case 1 corresponds to the force acting on the body, when the body is just about to move up.
Let’s consider the force acting on the body as ${ F }_{ 1 }$.

Similarly, case 2 corresponds to the force acting on the body to prevent it from slipping.
Let’s consider the force acting on the body in this case as ${ F }_{ 2 }$.
From the force body diagrams we have,
${ F }_{ 1 }=mg\sin { \theta } +{ f }_{ \mu }$
${{F}_{1}}=mg\sin \theta +\mu mg\cos \theta \to (1)$
${ F }_{ 2 }=mg\sin { \theta } -{ f }_{ \mu }$
${{F}_{2}}=mg\sin \theta -\mu mg\cos \theta \to (2)$
As per the given condition: ${ 2F }_{ 2 }={ F }_{ 1 }$.
Therefore, from eqn (1) and (2) we get,
$2(mg\sin { \theta } -\mu mg\cos { \theta } )=(mg\sin { \theta } +\mu mg\cos { \theta } )$
$mg\sin { \theta } =3\mu mg\cos { \theta }$
$\tan { \theta } =3\mu$
Therefore the inclination angle $\theta =\tan ^{ -1 }{ 3\mu }$.

Note: When making the force body diagram for these cases, always remember that the frictional force will be against the direction of motion of the body.
Here there are 2 very specific cases of direction of motion of the body, even though we are applying force along the same direction.