Question

The Fourier series of an odd periodic function, contains only
(A) Odd harmonics
(B) Even harmonics
(C) Cosine terms
(D) Sine terms

Answer 1

Hint: A Fourier series is a means of representing a periodic function as a sum of sine and cosine functions (possibly infinite).In such problems, finding zero coefficients is time consuming and can be prevented. With understanding of even and odd functions, without implementing the integration, the zero coefficient can be predicted.

Complete step by step answer:
A function $ y = f(t) $ is said to be odd if $ f( - t) = - f(t) $ for all values of $ t $ . The graph of an odd function is always symmetrical about the origin.
Let the odd function be $ f(t) = \sin t $
Then the graph of the following function will be represented as:

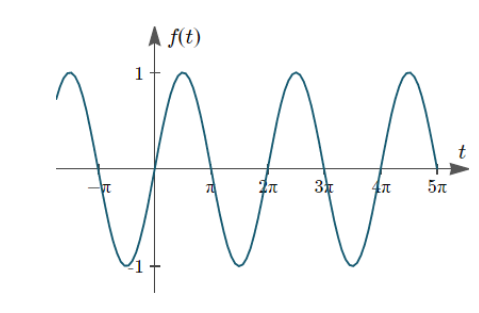
The above graph has amplitude $ 1 $ and period $ 2\pi $
For an odd function $ f(t) $ defined over the range $ - L $ to $ L $ (period $ = 2L) $
We can observe that $ {a_n} = 0 $ for all $ n $
Then we have
 $ {a_n} = \dfrac{1}{L}\int_{ - L}^L f (t)\cos \dfrac{{n\pi t}}{L}dt $
So, the zero coefficients in this case are: $ {a_0} = 0 $ and $ {a_n} = 0 $
The coefficients of $ {b_n} $ is given by
 $ {b_n} = \dfrac{1}{L}\int_{ - L}^L f (t)\sin \dfrac{{n\pi t}}{L}dt $
Therefore, the Fourier series of the following odd function is given by
 $ f(t) = \sum\limits_{n = 1}^\infty {{b_n}} \sin \dfrac{{n\pi t}}{L} $
Hence, the Fourier series of an odd periodic function contains only sine terms.
Hence the correct option is (D).

Note:
Using the Fourier series in various questions makes our task easy, fast, and more productive. We can easily find out the zero coefficient of vast problems by the help of Fourier series even without performing the actual integration. Baron Jean Baptiste Joseph Fourier introduced the idea that a series of harmonically related sines and cosines can represent any periodic function.