Question

The friction coefficient between the board and the floor shown in figure is $\mu$. Find the maximum force that the man can exert on the rope so that the board does not slip on the floor.

Answer 1

Hint: Frictional force has an upper limit based on the normal reaction on the surface. Unless the man applies force which will cross this upper limit, the board will not move. The same force is the maximum force that man should apply. Consider force balance on both objects starting from the man and find the normal reaction between the board and the ground.

Complete answer:
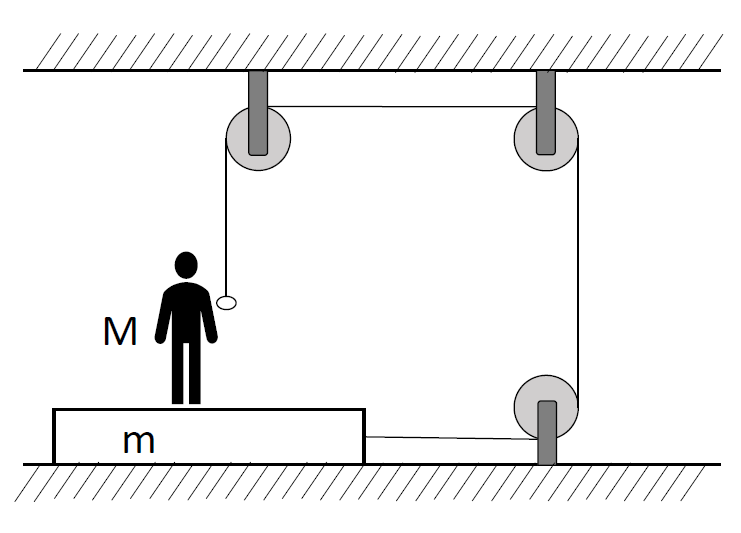
As per the diagram, we have been given two masses, $M$ of the man standing on a board of mass $m$. Net weight on the floor = Weight of man + Weight of the board
$= Mg + mg$
$= (M + m)g$
Here, $g$ is acceleration due to gravity directed in downward direction. As soon as there is a tendency of the board to move relative to the floor there will be frictional force exerted on the board-floor contact surface to resist the board's motion. The friction coefficient between the board and the floor is $\mu $. Therefore the maximum friction force which the floor can exert is $\mu N$, where $N$ is the normal reaction at the contact surface between the board and the floor. Since the floor is horizontal, this normal reaction is equal to the net weight on the surface. Therefore, $N = (M + m)g$ in upward direction.
Maximum frictional force on the board is given $ = \mu N = \mu (M + m)g$
But, one thing to notice is that as soon as man starts applying force, the net weight of the man on board will be reduced. Let the applied force be $F$.
So the net weight of man on board $ = Mg - F$
Normal reaction $N = (Mg - F + mg)$
At maximum application of force, frictional force will balance the force applied. Let the maximum force be ${F_m}$ and the relation will be as follows:
${F_m} = \mu (Mg - {F_m} + mg)$
Solving this equation for ${F_m}$, we get,
$\Rightarrow {F_m}(1 + \mu ) = \mu (M + m)g$
$\Rightarrow {F_m} = \dfrac{{\mu (M + m)g}}{{(1 + \mu )}}$
We are assuming the pulley wheels are smooth that means there is no additional friction due to their rolling. If they are specifically mentioned then additional terms will have to be considered in the force balance equation.

Note: Generally we make mistakes by not considering the force balance over man when force is applied since while pulling the rope down, the max experiences a force in upward direction thus affecting the weight of man on board. We may end up considering the total force on the floor as the algebraic sum of weight of man and board. This will lower the value of force applied by the man and thus incorrect.