Question

The frustum of a regular triangular pyramid has equilateral triangle for its bases. The lower and upper base edges are 9 m and 3 m respectively. If the volume is 118.2 cu. m, how far apart (m) are the bases?
(a) 9
(b) 8
(c) 7
(d) 10

Answer 1

Hint: First draw a rough figure of a frustum of a regular pyramid. Apply the formula for the volume of the frustum of pyramid given by: volume = $ \dfrac{h}{3}\left[ {{A}_{1}}+{{A}_{2}}+\sqrt{{{A}_{1}}{{A}_{2}}} \right] $ , where ‘h’ is the distance between the bases, $ {{A}_{1}} $ and $ {{A}_{2}} $ are the area of the base triangles which are equilateral. To determine the area of these triangles use the formula: $ A=\dfrac{\sqrt{3}}{4}{{a}^{2}} $ , where ‘A’ denotes the area and ‘a’ denotes the side of equilateral triangle. Finally, substitute all the given and obtained values in the expression of volume to get the value of ‘h’.

Complete step-by-step answer:

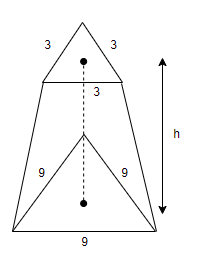
From the above figure of frustum of a pyramid, let us assume that the distance between the bases of the cone is ‘h’.
We know that volume of a frustum of pyramid is given as:
 $ V=\dfrac{h}{3}\left[ {{A}_{1}}+{{A}_{2}}+\sqrt{{{A}_{1}}{{A}_{2}}} \right] $ , where ‘V’ denotes the volume, ‘h’ is the distance between the bases, $ {{A}_{1}} $ and $ {{A}_{2}} $ are the area of the base triangles which are equilateral.
First let us find the area of the two equilateral triangles. Applying the formula for area of an equilateral triangle: $ A=\dfrac{\sqrt{3}}{4}{{a}^{2}} $ , where ‘A’ denotes the area and ‘a’ denotes the side of equilateral triangle we have,
 $ \begin{align}
  & (i){{A}_{1}}=\dfrac{\sqrt{3}}{4}\times {{3}^{2}} \\
 & (ii){{A}_{2}}=\dfrac{\sqrt{3}}{4}\times {{9}^{2}} \\
\end{align} $
Also, we have been given that the volume of the frustum is 118.2 cu. m. Hence, $ \left( V=118.2\text{ cu}\text{. m} \right) $ . Therefore, substituting all the value in the expression of volume of frustum, we get,
 $ \begin{align}
  & 118.2=\dfrac{h}{3}\left[ \dfrac{\sqrt{3}}{4}\times {{3}^{2}}+\dfrac{\sqrt{3}}{4}\times {{9}^{2}}+\sqrt{\dfrac{\sqrt{3}}{4}\times {{3}^{2}}\times \dfrac{\sqrt{3}}{4}\times {{9}^{2}}} \right] \\
 & \Rightarrow 118.2=\dfrac{h}{3}\times \dfrac{\sqrt{3}}{4}\left[ {{3}^{2}}+{{9}^{2}}+\sqrt{{{3}^{2}}\times {{9}^{2}}} \right] \\
 & \Rightarrow 118.2=\dfrac{h}{3}\times \dfrac{\sqrt{3}}{4}\left[ 9+81+27 \right] \\
 & \Rightarrow 118.2=\dfrac{h}{3}\times \dfrac{\sqrt{3}}{4}\left[ 117 \right] \\
 & \Rightarrow h=\dfrac{118.2\times 4\times 3}{\sqrt{3}\times 117} \\
 & \Rightarrow h=\dfrac{118.2\times 4\times \sqrt{3}}{117} \\
\end{align} $
Substituting, $ \sqrt{3}=1.732 $ , we get,
 $ h=\dfrac{118.2\times 4\times 1.732}{117} $
On simplification we get,
 $ \begin{align}
  & h=6.99 \\
 & \Rightarrow h\approx 7 \\
\end{align} $
Hence, option (c) is the correct answer.

Note: One may note that we have to apply the formula for the volume of a frustum of a pyramid and not for the frustum of a cone. The basic difference between the two is that, in frustum of cone, the bases are circular in shape while, in frustum of pyramid, the bases are triangular in shape. In the above solution, we have substituted the value of $ \sqrt{3}=1.732 $ to calculate the value of ‘h’.