
The given figure consists of a square, a quarter circle and a semicircle. Area of sector is
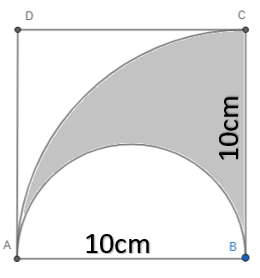

Answer
497.1k+ views
Hint:In the figure we can see that the perimeter of the shaded portion is the addition of the circumference of quarter circle and semicircle. We know that circumference of a semicircle is
Complete step by step answer:
Now consider the figure given
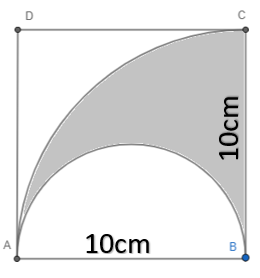
We have two parts of circles here one with radius AB and another with diameter AB. We can see that the Perimeter of the shaded portion will be the addition of circumference of both radius.
Now consider the Quarter circle with a radius 10cm. Now we know that circumference of the quarter circle is given by
Now here the radius is AB, BC and is equal to 10cm hence we get
Hence we have the circumference of the quarter-circle that is arc AC is
Now consider the semicircle with diameter AB.
Now we know that circumference of the semicircle is given by
Now we know that diameter = 2 × radius. Hence we have 2r = d
Substituting this we get
Now we know that the diameter of the semicircle is AB and is equal to 10cm
Hence we get the circumference of the semicircle is
Hence we have a circumference of a semicircle that is arc AB =
Now we know the perimeter of the shaded portion will be the addition to the circumference of both radii.
Hence from equation (1) and (2) we have
Perimeter of shaded portion is
Hence we get the perimeter of the shaded portion is
Option b is the correct option.
Note:
Note that the area of circle is given by
Complete step by step answer:
Now consider the figure given

We have two parts of circles here one with radius AB and another with diameter AB. We can see that the Perimeter of the shaded portion will be the addition of circumference of both radius.
Now consider the Quarter circle with a radius 10cm. Now we know that circumference of the quarter circle is given by
Now here the radius is AB, BC and is equal to 10cm hence we get
Hence we have the circumference of the quarter-circle that is arc AC is
Now consider the semicircle with diameter AB.
Now we know that circumference of the semicircle is given by
Now we know that diameter = 2 × radius. Hence we have 2r = d
Substituting this we get
Now we know that the diameter of the semicircle is AB and is equal to 10cm
Hence we get the circumference of the semicircle is
Hence we have a circumference of a semicircle that is arc AB =
Now we know the perimeter of the shaded portion will be the addition to the circumference of both radii.
Hence from equation (1) and (2) we have
Perimeter of shaded portion is
Hence we get the perimeter of the shaded portion is
Option b is the correct option.
Note:
Note that the area of circle is given by
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




