Question

The given figure shows a solid form of a solid cube of side 40cm and a solid cylinder of radius 20cm and a height 50cm attached to the cubes as shown. Find the volume and the total surface area of the whole solid [Take$\pi = 3.14$]

A. $122700c{m^3}$and $15880c{m^2}$
B. $126800c{m^3}$and $15880c{m^2}$
C. $148900c{m^3}$and $15880c{m^2}$
D. $148800c{m^3}$and $15880c{m^2}$

Answer 1

Hint: We have given the dimension of the cube and the cylinder, first, we’ll find the volume of the complete solid by adding the volume of individual solid. Now, we’ll find the total surface area by adding the individual surface area neglecting the area of the joint surface.

Complete step by step answer:

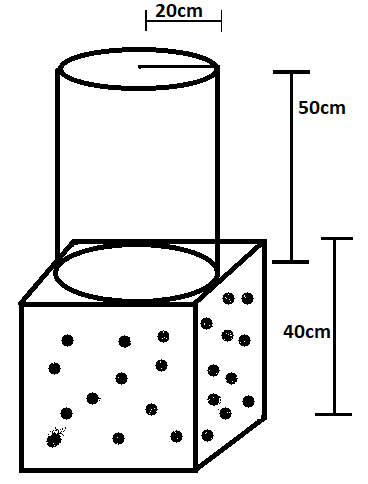
Given: side of the cube$ = 40cm$
The radius of the base of the cylinder$ = 20cm$
The height of the cylinder$ = 50cm$
We know that the volume of the cube$ = {\left( {side} \right)^3}$
The volume of the cylinder$ = \pi {(radius)^2}height$
Therefore the volume of the solid$ = $ volume of the cylinder$ + $ volume of the cube
$ = \pi {(20)^2}50 + {(40)^3}$
Solving the square and the cube
$ = \pi (400)50 + (64000)$
Substituting $\pi = 3.14$
$ = 3.14(20000) + 64000$
$ = 62800 + 64000$
Therefore total volume$ = 126800c{m^3}$
Similarly, the total surface area of the cylinder$ = 2\pi (radius)\left[ {radius + height} \right]$
And the total surface area of the cube$ = 6{(side)^2}$
But for the area of the surface joining the cylinder and the cube should not be included as they are not in the outer part of the complete solid figure.
Total surface area$ = $total surface area of cube$ + $total surface of the cylinder$ - 2$(base area of the cylinder)
$ = 6{(40)^2} + 2\pi (20)(20 + 50) - 2\pi {(20)^2}$
Solving the squares
$ = 6(1600) + 40\pi (70) - 2\pi (400)$
Simplifying the brackets and substituting$\pi = 3.14$
\[ = 9600 + 2800(3.14) - 3.14(800)\]
Again simplifying the brackets
$ = 9600 + 8792 - 2512$
Therefore the total surface area of solid$ = 15880c{m^2}$
Option(B) is correct.

Note: While finding the total surface area most of the students subtract the area of the common surface once, but should be subtracted twice as we have included that area from both the solid, so keep this in mind to examine the solid carefully then start solving questions like this.