Question

The given graph represents the variation of Z (compressibility factor = \[\dfrac{{PV}}{{nRT}}\] ) versus P, for three real gases A, B and C. Identify the only incorrect statement.

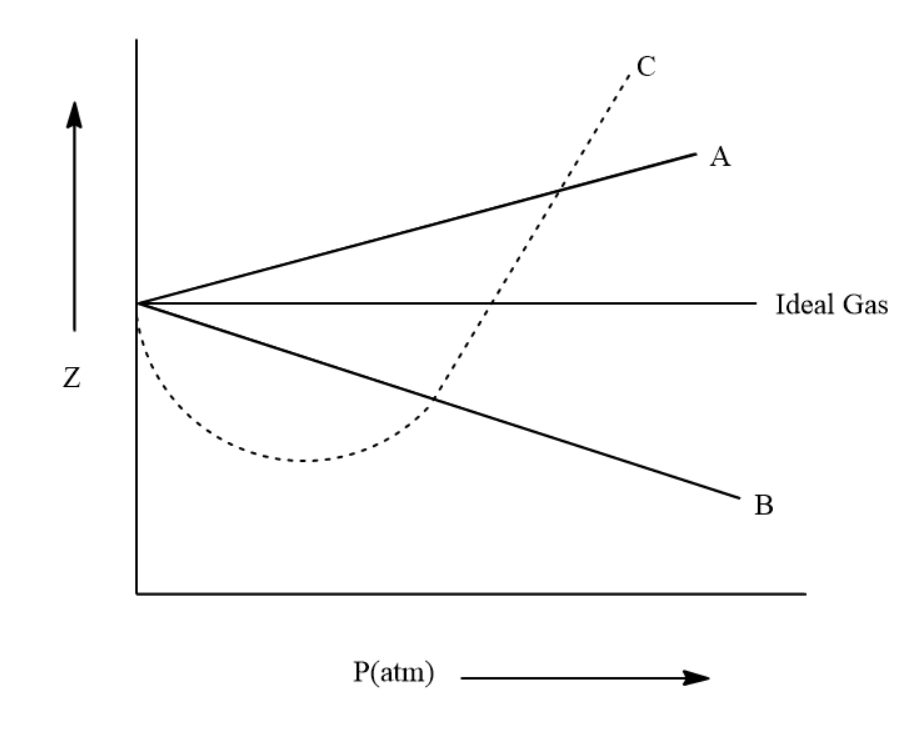
A.For the gas A, a=0 and its dependence on P is linear at all pressure
B.For the gas B, b=0 and its dependence on P is linear at all pressure
C.For the gas C, which is typical real gas for which neither a nor b = 0. By knowing the minima and the point of intersection, with Z = 1, a and b can be calculated
D.At high pressure, the slope is positive for all real gases

Answer 1

Hint: To solve this question, we need to study the characteristics of real gases. According to the van der Waal equation for real gases a and b are constants of attraction and volume respectively. At low pressure we can neglect the comparison to a very large volume and thus we can find the correct option for the given graph.

Complete answer: Let,
According to a real gas equation, the constants 'a' and 'b' are Van der Waals constants for attraction 'a' and volume 'b' are characteristic constants for a given gas.
The 'a' value for a given gas is a measure of intermolecular forces of attraction. As the intermolecular forces of attraction increases, more will be the value of a.
For a given gas van der Waals constant of attraction 'a' is always greater than van der Waals constant of volume 'b'.
The gas having a higher value of ‘a’ can be liquefied easily and therefore hydrogen ​ and Helium is not easily liquefiable.
Based on the above observations we can say that for gas A (Z > 1), a=0 and its dependence on P is linear at all pressures. Also, at high pressure, the slope is positive for all real gases and thus option D is also correct.
Thus we can say that the incorrect statement is Option (B).

Note:
Another way of solving this is by using the following method. From the graph it is clear that the value of z decreases with the increase of pressure. We can explain this using the van der Waals' equation. At high pressure, when the pressure is large, volume will be small and one cannot ignore 'b' in comparison to V. This means that z is greater than one and it increases linearly with pressure.