Question

The glancing angle of incidence is ${{10}^{\circ }}$. What will be the glancing angle of reflection?
$\text{A}\text{. 1}{{0}^{\circ }}$
$\text{B}\text{. 8}{{0}^{\circ }}$
$\text{C}\text{. 17}{{0}^{\circ }}$
$\text{D}\text{. 6}{{0}^{\circ }}$

Answer 1

Hint: When a ray of light hits a surface, it gets bounced back from the surface and this we call as reflection of light. If the surface where light ray is being incident is smooth, it follows some laws of reflection. We will study the laws of reflection and will find the relation between various angles, such as angle of incidence, glancing angle of incidence, angle of reflection, and glancing angle of reflection.

Complete step by step answer:
Reflection is defined as the change in direction of a wavefront at an interface between two media, so that after reflection the wavefront returns into the same medium from which it was originated. When a light ray approaches a smooth polished surface and it bounces back from the surface, it is known as Reflection of light. The ray which lands upon the surface is called the incident ray and the ray after bouncing back from the surface is called a Reflected surface. If we draw a perpendicular on the reflecting surface, it is called normal.

Representation of Reflection of light:

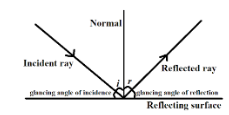
The laws of reflection determine how a light ray would be bent after being incident on reflecting surfaces such as mirrors and smooth metal surfaces.

Laws of reflection:

The incident ray, the reflected ray and the normal, all lie in the same place.
The angle of incidence is always equal to the angle of reflection.

Glancing angle of incidence is defined as the angle between the ray which is incident on the surface and that surface itself. As we know incident angle is the angle between the incident ray and the normal, it means that the sum of incident angle and glancing angle of incidence will always be ${{90}^{\circ }}$. We can also say that a glancing angle of incidence is the complement of incident angle, or the incident angle is the complement of glancing angle of incidence. The same equation is true for angle of reflection and glancing angle of reflection. Angles of reflection and glancing angles of reflection are complement to each other.
If two angles are complementary, their sum is always equal to${{90}^{\circ }}$.
Let’s take incident angle as $i$,
We get a glancing angle equal to ${{90}^{\circ }}-i$ .
Given that glancing angle of incidence equals${{10}^{\circ }}$
Therefore,
Angle of incidence, that is, $i={{90}^{\circ }}-\text{ glancing angle of incidence}$

$\begin{align}
  & i={{90}^{\circ }}-{{10}^{\circ }} \\
 & i={{80}^{\circ }} \\
\end{align}$

$\text{Angle of incidence = }{{90}^{\circ }}$

According to the law of reflection, angle of incidence is always equal to the angle of reflection.
Therefore, we get,
Angle of reflection $r={{80}^{\circ }}$
Glancing angle of reflection will be complement to angle of reflection
Therefore,

$\text{glancing angle of reflection = }{{90}^{\circ }}-r$
$\text{glancing angle of reflection = }{{90}^{\circ }}-{{80}^{\circ }}={{10}^{\circ }}$
The glancing angle of reflection is${{10}^{\circ }}$.

Hence, the correct option is A.

Note:
According to the laws of reflection, the angle of incidence is always equal to the angle of reflection. Also, we have a glancing angle of incidence that is complement to angle of reflection and glancing angle of reflection is complement to angle of reflection. If angle of incidence is equal to angle of reflection, it means that glancing angle of incidence is always equal to glancing angle of reflection. This equation can be applied in such questions to obtain the answer directly.