Question

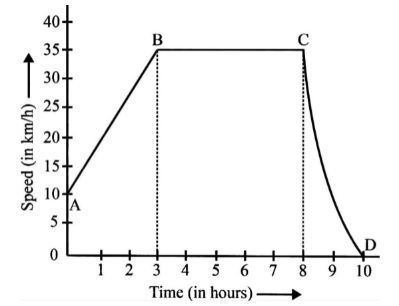
The graph given alongside shows how the speed of the car changes with time.
(i) What is the initial speed of the car?
(ii) What is the maximum speed attained by car?
(iii) Which part of the graph shows zero acceleration?
(iv) Which part of the graph shows varying retardation?
(v) Find the distance travelled in the first 8 hours.

Answer 1

Hint:When representing the movement of an object, speed-time graphs are quite useful. They can be used to determine whether an object is moving or not at any given time. They can also be used to determine the speed at which an object is moving at any given time. We can calculate any acceleration, change in speed, and change in time using data from the graph. We can also utilise graphs to figure out how far we've travelled. The distance travelled is represented by the area under a speed-time graph.

Complete step by step answer:
(i) The car's initial speed is the speed at \[t = 0\] . As a result, the speed is \[10{\text{ }}km{h^{ - 1}}\] .
(ii) The maximum speed is \[35km{h^{ - 1}}\] . Look at points B and C.
(iii) Because the car's speed does not change with time, B to C exhibits zero acceleration.
(iv) Because the speed of the component from C to D does not decrease uniformly with time, it shows variable retardation. (You can see that we have uniform acceleration from part A to part B.)
(v) You must compute the area below AB and BC, which is, to determine the distance travelled in the first 8 hours.
$\Rightarrow \left( {35 - 10} \right) \times \dfrac{3}{2} + 35 \times 5 \\
\Rightarrow 37.5 + 175 = 212.5km \\ $
You can also use the equations of motion to figure it out. Let me use the equations of motion to compute the distance between A and B.
Initial velocity $\left( u \right) = 10\,k{h^{ - 1}}$
Final velocity $\left( v \right) = 35\,km{h^{ - 1}}$
Time $ = 3hr$
\[a{\text{ }} = \dfrac{{\left( {{\text{ }}v - u} \right)}}{t}{\text{ }} = {\text{ }}\dfrac{{\left( {35 - 10} \right)}}{3} = {\text{ }}\dfrac{{25}}{3}\]
$\Rightarrow {v^2} = {u^2} + 2as$

Therefore, from this equation we will evaluate the value of $'s'$
$s = \dfrac{{\left( {{v^2} - {u^2}} \right)}}{{2a}} \\
\Rightarrow s = \dfrac{{\left\{ {{{\left( {35} \right)}^2} - {{\left( {10} \right)}^2}} \right\}}}{{2 \times 8.33}} \\
\therefore s = 67.5 $
When we add up all of the numbers, we get \[s = {\text{ }}67.5{\text{ }}km\], which is the same as the area of the trapezoid produced below AB. That indicates the moderators marked my answer incorrectly when I was correct. As a result, the total distance is \[67.5 + 175 = 242.5{\text{ }}km\] .The answer \[212.5{\text{ }}km\] is erroneous; the correct answer is \[242.5{\text{ }}km\].

Note:A constant speed is represented by a horizontal line on a speed-time graph. An acceleration is represented by a sloping line on a speed-time graph. The sloping line indicates that the object's speed is changing. The object is either accelerating or decelerating.