Question

The graph of the $f\left( x \right)$ is shown below. Graph each transformed function and list in words the transformation used?

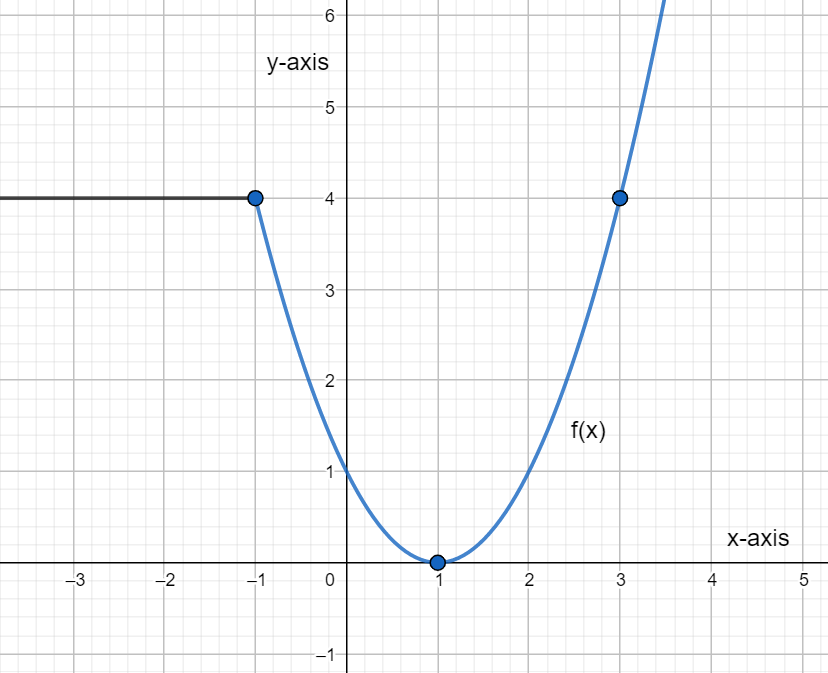
a) $g\left( x \right)=f\left( -x \right)+1$
b) $h\left( x \right)=-\dfrac{1}{2}f\left( x \right)-2$
c) $k\left( x \right)=2f\left( x+3 \right)-1$

Answer 1

Hint: To solve this question, we need to know the various transformations in mathematical functions. We show each of the given transformations used for the given function $f\left( x \right)$ and plot the corresponding graphs. For the first part, we use reflection and vertical translation. For the second part, we have done a vertical shrink or compression and also a vertical translation downwards. For the last part, we have used vertical enlarge and horizontal translation. The graphs of the same are plotted.

Complete step by step solution:
In order to solve such questions, it is very important to know the concept of transformations and how to visually represent these transformations, that is graphically.
Given in the question is the graph for the function denoted by $f\left( x \right).$ We now perform some transformations as specified in the question.
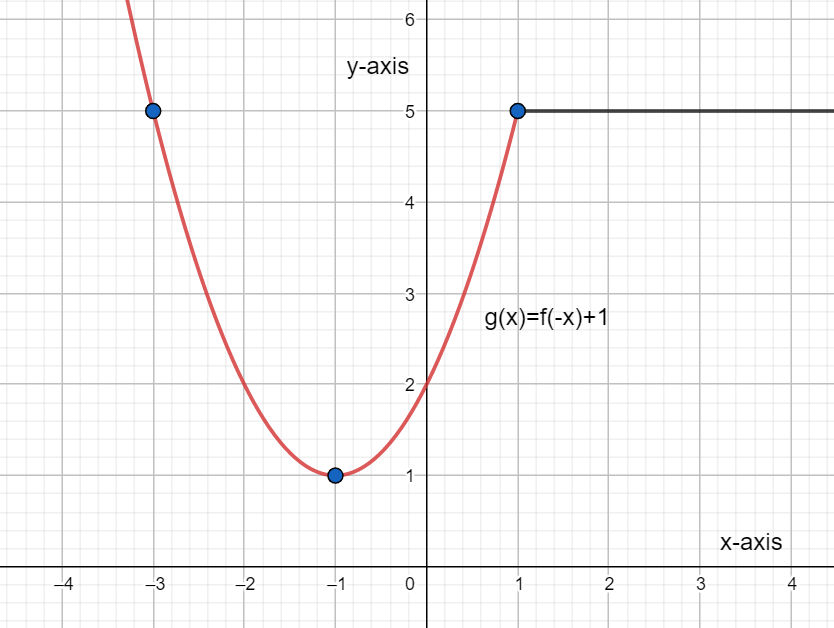
Firstly, we have the transformed function represented as $g\left( x \right)=f\left( -x \right)+1.$ For this, the graph has been plotted as shown below. For this graph, there is a reflection with respect to the y-axis as indicated by the negative sign of x in the equation and it is vertically translated by 1 unit upwards.

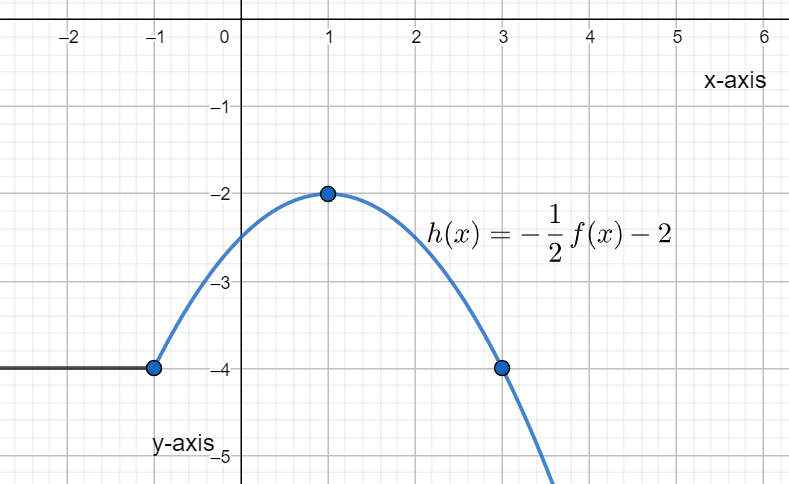
For the second part, we have the function given as $h\left( x \right)=-\dfrac{1}{2}f\left( x \right)-2.$ We have performed a vertical compression or shrinking by half or $\dfrac{1}{2}.$ We have also reflected the curve with respect to x-axis as indicated by the negative sign before $f\left( x \right).$ Then we also have performed a vertical translation of 2 units downwards.

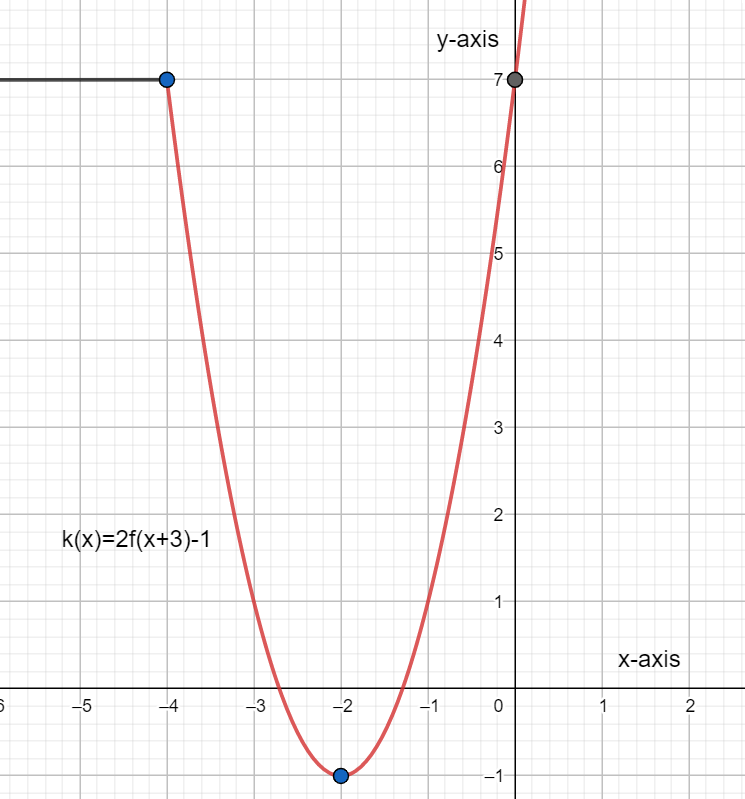
 For the last part, the function given is $k\left( x \right)=2f\left( x+3 \right)-1.$ Here, we have vertically enlarged the function by 2 times and we have horizontally translated it by 3 units to the left. We have also vertically translated it 1 unit downwards.

Hence, we have plotted the graph for each transformation and specified the transformation used for each stage too.

Note: It is essential to know the basic transformation functions in mathematics. Translation means to move the graph in any direction without altering its shape or size. Compression or enlargement alters the size of the graph and does not move it from its location. Reflection with respect to any axis is just a mirror image of the graph with respect to the axis along which it is reflected.