Question

The graph of the lines $x + y = 7$ and $x - y = 3$ meet at the point-
A. $\left( {5,2} \right)$
B. $\left( {2,5} \right)$
C. $\left( {6,3} \right)$
D. $\left( { - 1,4} \right)$

Answer 1

Hint- From the given equations, find out the value of y and then start putting the values of x (let’s say 1,2,3) to find out the value of y when x was 1 or 2 or 3. Do the same in the second equation as well and find out the common points in both the values of the equations.

Complete Step-by-step answer:

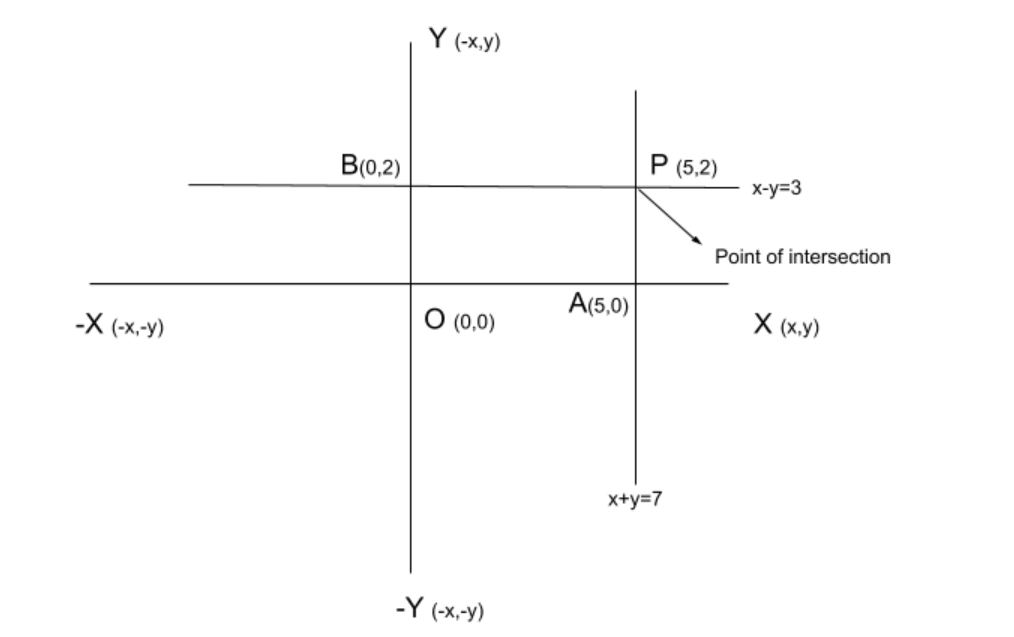
The equations given in the question are-
$x + y = 7$
And
$x - y = 3$
Let’s mark both the equations as 1 and 2. We have-
$x + y = 7$ $ \to $ equation 1
And
$x - y = 3$ $ \to $ equation 2
For equation 1, the value of y will be-
$y = 7 - x$
Marking the recent equation as equation 3, we have-
$y = 7 - x$ $ \to $ equation 3
Now, for equation 3, we will put the value of x as 1,2 or 3. Every time, we will get a new value of y:
If $x = 1$, then the value of y will be $y = 7 - 1 = 6$
If $x = 2$, then the value of y will be $y = 7 - 2 = 5$
If $x = 3$, then the value of y will be $y = 7 - 3 = 4$

Now, for equation 2 which is $x - y = 3$, the value of y will be as follows-
$y = x - 3$
Marking the above equation as equation 4, we have-
$y = x - 3$ $ \to $ equation 4
Now, again, for equation 4, we will put different values of x to get different values of y:
If $x = 1$, then the value of y will be $y = 1 - 3 = - 2$
If $x = 2$, then the value of y will be $y = 2 - 3 = - 1$
If $x = 3$, then the value of y will be $y = 3 - 3 = 0$
If $x = 4$, then the value of y will be $y = 4 - 3 = 1$
If $x = 5$, then the value of y will be $y = 5 - 3 = 2$
In both the equations, equation 3 and equation 4, $x = 5,y = 2$ is common. Thus, we draw a graph and it meets the point $\left( {5,2} \right)$.

Note: While looking for the value of y, keep putting the value of x as 1,2,3 or 4 as long as one common value doesn’t appear. If you mark the equations, remember to put the number of the equation correctly and be careful with the negative and positive signs.