
The gravitational field in a region is
A.2x+3y=c
B.2y+3x=c
C.X+2y=c
D.1.5x+2y=c
Answer
493.2k+ views
Hint: Recall that the equipotential line traces all point at the same gravitational potential. This means that the equipotential line is perpendicular to the gravitational field lines. From this perspective, find the slope of the field vector given to us. Then, find the corresponding slope of the equipotential line by taking the negative reciprocal of the slope of the field vector. Then substitute this into the straight line equation and you should arrive at the equipotential line equation.
Formula Used:
Slope of a line perpendicular to a line of slope m:
Equation of a straight line:
Complete answer:
We know that an equipotential line is the line along which the gravitational potential is constant. They provide a quantitative way of viewing the gravitational potential in two dimensions. Every point on this line will be at the same potential. In three dimensions, the lines from equipotential surfaces. Moving along an equipotential surface requires no work because this movement is always perpendicular to the gravitational field.
Let the equation of the equipotential line be
We know that the equipotential line is always perpendicular to the gravitational field lines.
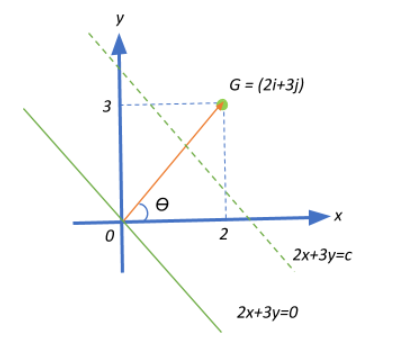
Given that
Now, since the equipotential line will be perpendicular to the gravitational field, the slope of the equipotential line will be the negative reciprocal of the slope of the gravitational field vector, i.e.,
Substituting this into our equipotential line equation:
Therefore, the correct choice would be A.
Note:
Note that though we got only one equation for the equipotential line, by varying the value of c we can get an infinite number of equipotential lines that are all perpendicular to the gravitational field. Thus, there is not one but many equipotential lines that are obtained for a given range of gravitational fields.
Formula Used:
Slope of a line perpendicular to a line of slope m:
Equation of a straight line:
Complete answer:
We know that an equipotential line is the line along which the gravitational potential is constant. They provide a quantitative way of viewing the gravitational potential in two dimensions. Every point on this line will be at the same potential. In three dimensions, the lines from equipotential surfaces. Moving along an equipotential surface requires no work because this movement is always perpendicular to the gravitational field.
Let the equation of the equipotential line be
We know that the equipotential line is always perpendicular to the gravitational field lines.

Given that
Now, since the equipotential line will be perpendicular to the gravitational field, the slope of the equipotential line will be the negative reciprocal of the slope of the gravitational field vector, i.e.,
Substituting this into our equipotential line equation:
Therefore, the correct choice would be A.
Note:
Note that though we got only one equation for the equipotential line, by varying the value of c we can get an infinite number of equipotential lines that are all perpendicular to the gravitational field. Thus, there is not one but many equipotential lines that are obtained for a given range of gravitational fields.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 Economics: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Write a short note on Franklands reaction class 12 chemistry CBSE

The amine A when treated with nitrous acid gives yellow class 12 chemistry CBSE

A ray of light is incident normally on the surface class 12 physics CBSE

An example of ex situ conservation is a Sacred grove class 12 biology CBSE

Who discovered the cell and how class 12 biology CBSE




