Question

The gravitational field strength $\vec{E}$ and the gravitational potential $\vec{V}$ are related as $\vec{E}=-\left( \dfrac{\partial V}{\partial x}\hat{i}+\dfrac{\partial V}{\partial y}\hat{j}+\dfrac{\partial V}{\partial z}\hat{k} \right)$. In the figure the transversal line represents equipotential surfaces. A particle of mass m is released from rest at the origin. The gravitational unit of potential, $1\vec{V}=1c{{m}^{2}}\,{{s}^{-2}}$. X-component of velocity of the particle at the point $(4cm,4cm)$ is-

(A). $4cm\,{{s}^{-1}}$
(B). $2cm\,{{s}^{-1}}$
(C). $2\sqrt{2}cm\,{{s}^{-1}}$
(D). $1cm\,{{s}^{-1}}$

Answer 1

Hint: The relation between electric field and potential is given. It represents that the electric field along any axis is the change in potential per unit change in distance along the axis. Using the relation we can calculate the electric field at a point. Using the electric field we can calculate the acceleration and then calculate the velocity of the particle using equations of motion.
Formulas used:
$E=-\dfrac{\Delta V}{\Delta x}$
$F=mE$
$F=ma$
${{v}^{2}}={{u}^{2}}+2as$

Complete answer:
The electric field is defined as the work done to bring a unit charge from infinity to a point in the field. Its SI unit is $V\,{{m}^{-1}}$.
The electric potential is defined as the work done to move a unit charge from one point to the other in an electric field. Its SI unit is volt ($V$).
Given that relationship between electric field and electric potential is $\vec{E}=-\left( \dfrac{\partial V}{\partial x}\hat{i}+\dfrac{\partial V}{\partial y}\hat{j}+\dfrac{\partial V}{\partial z}\hat{k} \right)$.
This means that along every axis the electric field is the change in potential per unit change in distance along the axis. Therefore, electric field along x-axis is
$E=-\dfrac{\Delta V}{\Delta x}$ - (1)
Here, $\Delta V$ is the change in potential between two points
$\Delta x$ is the distance between two points
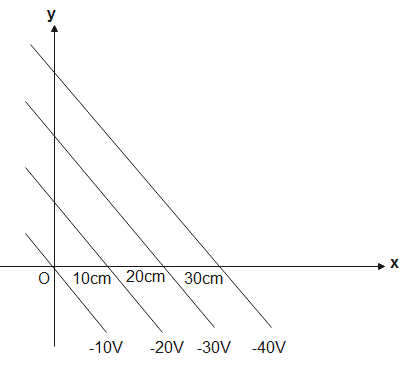
The electric lines of forces are perpendicular to the equipotential surface. Let us assume that the particle is positively charged then it will follow the path a shown

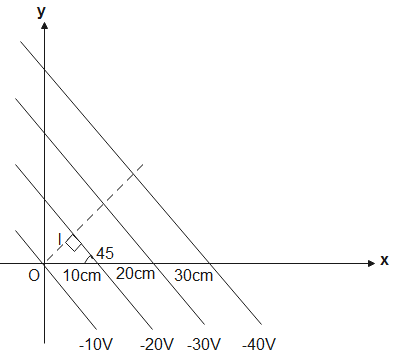
The dash line represents the path followed by the particle. According to the figure,
$\begin{align}
  & \Delta V=-20-(-10) \\
 & \therefore \Delta V=-10V \\
\end{align}$
$\begin{align}
  & l=10\cos {{45}^{o}} \\
 & \Rightarrow l=\dfrac{10}{\sqrt{2}}cm \\
\end{align}$
We know that, $l=\Delta x$. We substitute given values in eq (1), to get
$\begin{align}
  & E=-\dfrac{-10}{\dfrac{10}{\sqrt{2}}} \\
 & \Rightarrow E=\sqrt{2}V{{m}^{-1}} \\
\end{align}$
The electric field is $\sqrt{2}V{{m}^{-1}}$
We know that,$F=mE$ - (2)
Here, $F$ is the force acting on the charge particle
$m$ is the mass of the particle
Also, $F=ma$ - (3)
Here, $m$ is the mass of the particle
$a$ is the acceleration of the particles
From eq (2) and eq (3), we get,
$\begin{align}
  & mE=ma \\
 & \Rightarrow E=a \\
\end{align}$
Substituting given values in the above equation, we get,
$\sqrt{2}=a$
Therefore, the acceleration of the particle is $\sqrt{2}cm{{s}^{-2}}$
The particle is under constant acceleration as the force acting on it is constant. We can apply the following equation of motion
${{v}^{2}}={{u}^{2}}+2as$
Here, $v$ is the final velocity
$u$ is the initial velocity
$s$ is the distance travelled
Given, $u=0,\,s=x=4cm$. Substituting in the above equation we get,
$\begin{align}
  & {{v}^{2}}=0+2\sqrt{2}\times 4 \\
 & \Rightarrow {{v}^{2}}=8\sqrt{2} \\
 & \therefore v\approx 2\sqrt{2}cm\,{{s}^{-1}} \\
\end{align}$
Therefore, the x-component of velocity is $2\sqrt{2}cm\,{{s}^{-1}}$.

Hence, the correct option is (C).

Note:
In partial differentiation, other variables other than the variable with respect to which we differentiate are taken constant. The equipotential surfaces can be open or closed but the electric lines of forces are always open. On every point of an equipotential surface, the potential is the same.