
The harmonic mean of the segments of a focal chord of \[{{y}^{2}}=8x\] .
A. 16
B. 5
C. 8
D. 4
Answer
597k+ views
Hint: By comparing \[{{y}^{2}}=8x\] and general equation of parabola ${{y}^{2}}=4ax$ , find the value of a. the harmonic mean of 2 no: x & y is of the form $\dfrac{2}{\dfrac{1}{x}+\dfrac{1}{y}}$ . The coordinate of A & B of focal chord are of the form $\left( a{{t}^{2}},2at \right)$ and focus S. Thus harmonic mean will be $\dfrac{2}{\dfrac{1}{AS}+\dfrac{1}{BS}}$ . Thus find AS & BS, simplify it to get the harmonic mean.
Complete step-by-step answer:
We have been given the equation of parabola as \[{{y}^{2}}=8x\]. Now by comparing both general equation and the given equation of the parabola, we cans say that the latus rectum = 4a=8
$\begin{align}
& a=\dfrac{8}{4}=2 \\
& \text{i}\text{.e}\text{. }a=2 \\
\end{align}$
Hence we get a=2.
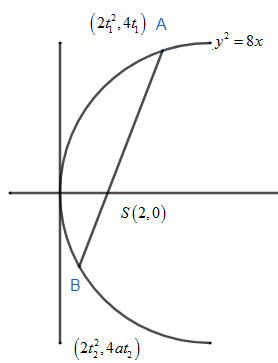
From the figure we can say that $S\left( 2,0 \right)$ is the focus of parabola \[{{y}^{2}}=8x\] .AB is the focal chord of the parabola. Let us take the coordinate of A and B as, put a=2,
$A\left( at_{1}^{2},2a{{t}_{1}} \right)$ and $B\left( at_{2}^{2},2a{{t}_{2}} \right)\Rightarrow $ \[~A\left( 2t_{1}^{2},4{{t}_{1}} \right)\] and $B\left( 2t_{2}^{2},4a{{t}_{2}} \right)$ .
Now, we have been asked to find the harmonic mean of the segment of the focal chord i.e. we need to find the harmonic mean of AS and SB from the figure. The harmonic mean of two numbers x and y are written as, $\dfrac{2}{\dfrac{1}{x}+\dfrac{1}{y}}$ .
Similarly the harmonic mean of AS and BS are written as $\dfrac{2}{\dfrac{1}{AS}+\dfrac{1}{BS}}$ .
Hence from the figure we can say, $AS=2t_{1}^{2}+2$ , $BS=2t_{2}^{2}+2$ .
$\therefore $ Harmonic mean $=\dfrac{2}{\dfrac{1}{AS}+\dfrac{1}{BS}}=\dfrac{2}{\dfrac{1}{2\left( t_{1}^{2}+1 \right)}+\dfrac{1}{2\left( t_{2}^{2}+1 \right)}}=\dfrac{2\times 2}{\dfrac{1}{\left( t_{1}^{2}+1 \right)}+\dfrac{1}{\left( t_{2}^{2}+1 \right)}}$ .
$\therefore $ We got the harmonic means as $\dfrac{4}{\dfrac{1}{t_{1}^{2}+1}+\dfrac{1}{t_{2}^{2}+1}}$ .
Here slope of AS= slope of BS
Thus for a focal chord ${{t}_{1}}{{t}_{2}}=-1$ thus, ${{t}_{2}}=-{{t}_{1}}-\dfrac{2}{{{t}_{1}}}$ .
Let us put this in the equation of harmonic means
$\therefore $ Harmonic mean $\dfrac{4}{\dfrac{1}{t_{1}^{2}+1}+\dfrac{1}{\dfrac{-1}{{{\left( {{t}_{1}} \right)}^{2}}}+1}}=\dfrac{4}{\dfrac{1}{t_{1}^{2}+1}+\dfrac{t_{1}^{2}}{1+t_{1}^{2}}}=\dfrac{4\left( 1+{{t}^{2}} \right)}{\left( 1+{{t}^{2}} \right)}=4$
Thus we got the harmonic mean of the segment of the focal chord as 4.
$\therefore $ Option (D) is the correct answer.
Note: The harmonic mean can be expressed as the reciprocal of the arithmetic mean. Thus, the harmonic mean of segments in the area of parabola means the harmonic mean of AS and BS i.e. of the focal chord AB.
Complete step-by-step answer:
We have been given the equation of parabola as \[{{y}^{2}}=8x\]. Now by comparing both general equation and the given equation of the parabola, we cans say that the latus rectum = 4a=8
$\begin{align}
& a=\dfrac{8}{4}=2 \\
& \text{i}\text{.e}\text{. }a=2 \\
\end{align}$
Hence we get a=2.
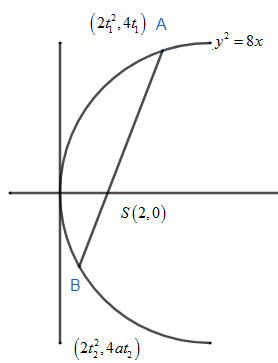
From the figure we can say that $S\left( 2,0 \right)$ is the focus of parabola \[{{y}^{2}}=8x\] .AB is the focal chord of the parabola. Let us take the coordinate of A and B as, put a=2,
$A\left( at_{1}^{2},2a{{t}_{1}} \right)$ and $B\left( at_{2}^{2},2a{{t}_{2}} \right)\Rightarrow $ \[~A\left( 2t_{1}^{2},4{{t}_{1}} \right)\] and $B\left( 2t_{2}^{2},4a{{t}_{2}} \right)$ .
Now, we have been asked to find the harmonic mean of the segment of the focal chord i.e. we need to find the harmonic mean of AS and SB from the figure. The harmonic mean of two numbers x and y are written as, $\dfrac{2}{\dfrac{1}{x}+\dfrac{1}{y}}$ .
Similarly the harmonic mean of AS and BS are written as $\dfrac{2}{\dfrac{1}{AS}+\dfrac{1}{BS}}$ .
Hence from the figure we can say, $AS=2t_{1}^{2}+2$ , $BS=2t_{2}^{2}+2$ .
$\therefore $ Harmonic mean $=\dfrac{2}{\dfrac{1}{AS}+\dfrac{1}{BS}}=\dfrac{2}{\dfrac{1}{2\left( t_{1}^{2}+1 \right)}+\dfrac{1}{2\left( t_{2}^{2}+1 \right)}}=\dfrac{2\times 2}{\dfrac{1}{\left( t_{1}^{2}+1 \right)}+\dfrac{1}{\left( t_{2}^{2}+1 \right)}}$ .
$\therefore $ We got the harmonic means as $\dfrac{4}{\dfrac{1}{t_{1}^{2}+1}+\dfrac{1}{t_{2}^{2}+1}}$ .
Here slope of AS= slope of BS
Thus for a focal chord ${{t}_{1}}{{t}_{2}}=-1$ thus, ${{t}_{2}}=-{{t}_{1}}-\dfrac{2}{{{t}_{1}}}$ .
Let us put this in the equation of harmonic means
$\therefore $ Harmonic mean $\dfrac{4}{\dfrac{1}{t_{1}^{2}+1}+\dfrac{1}{\dfrac{-1}{{{\left( {{t}_{1}} \right)}^{2}}}+1}}=\dfrac{4}{\dfrac{1}{t_{1}^{2}+1}+\dfrac{t_{1}^{2}}{1+t_{1}^{2}}}=\dfrac{4\left( 1+{{t}^{2}} \right)}{\left( 1+{{t}^{2}} \right)}=4$
Thus we got the harmonic mean of the segment of the focal chord as 4.
$\therefore $ Option (D) is the correct answer.
Note: The harmonic mean can be expressed as the reciprocal of the arithmetic mean. Thus, the harmonic mean of segments in the area of parabola means the harmonic mean of AS and BS i.e. of the focal chord AB.
Recently Updated Pages
Master Class 11 Chemistry: Engaging Questions & Answers for Success

Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




