Question

The heap of wheat is in the form of a cone whose diameter is $48m$ and height is $7m$. Find the volume of the heap. If it is covered by canvas to protect it from rain. Find the cost of the canvas required. Given that the rate of canvas is $Rs.7\,per\,100c{m^2}$.

Answer 1

Hint: The area can be defined as the space occupied by a flat surface of an object. The area is the number of unit squares closed by figure. Perimeter is the total length of the sides of the two dimensional shape. Perimeter is always less than the area of the given figure. Because the perimeter is outer and the area is inner property. Volume is the capacity which hold by objects
As we know that
$\therefore V = \dfrac{1}{3}\pi {r^2}h$
Here
V=volume
r=radius
h=height

Complete step-by-step solution:

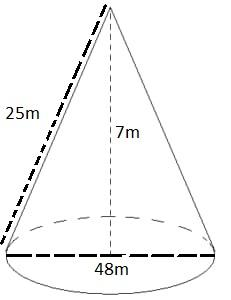
Given,
Diameter of heap,$d = 48m$
Radius of heap, $r = \dfrac{{48}}{2}m$
Radius of heap, $r = 24m$
Height of heap, $h = 7m$
Rate of canvass $Rs.7\,per\,100c{m^2}$
Volume=?
Slant height of heap, $l = ?$
As we know that
$\therefore l = \sqrt {{h^2} + {r^2}} $
Put the value
$ \Rightarrow l = \sqrt {{7^2} + {{24}^2}} $
$ \Rightarrow l = \sqrt {49 + 576} $
$ \Rightarrow l = \sqrt {625} $
$ \Rightarrow l = 25m$
Now the volume of heap
As we know that
$\therefore V = \dfrac{1}{3}\pi {r^2}h$
Put the value
$ \Rightarrow V = \dfrac{1}{3} \times \dfrac{{22}}{7} \times {(24)^2} \times 7$
Simplify
$ \Rightarrow V = 22 \times 24 \times 8$
$ \Rightarrow V = 4224{m^3}$
Now area covered by canvas
As we know that
$\therefore A = \pi rl$
Put the value
$ \Rightarrow A = \dfrac{{22}}{7} \times 24 \times 25$
Simplify
$ \Rightarrow A = \dfrac{{13200}}{7}$
$ \Rightarrow A = 1885.71{m^2}$
Now
The price of canvas,
$ \Rightarrow \text{Price of canvas} = \text{Area covered} \times \text{Rate of canvas}$
Put the value
$ \Rightarrow \text{Price of canvas} = 1885.71 \times \dfrac{7}{{100}}$
$1{m^2} = 10000c{m^2}$
$ \Rightarrow \text{Price of canvas} = 1885.71 \times \dfrac{7}{{100}} \times 10000$
$ \Rightarrow \text{Price of canvas} = Rs.1320000$

Note: The slant height of an object (such as frustum, cone, and pyramid) is the distance measured along a lateral face from the base to the apex along the “center” of the face. As we know that the slant height is given by
$\therefore l = \sqrt {{h^2} + {r^2}} $
Here
h=height of cone
r=base radius of cone
Here slant height is important to find the curved surface area of the cone, curved surface area means the area of surface which we can touch(outer surface).