The height of a cone is $20cm$ . A small cone is cut off from the top by a plane parallel to the base. If its volume is $\dfrac{1}{{125}}$ of the volume of the original cone, determine at what height above the base the section is made.
Answer
Verified360.9k+ views
Hint- Use the basic formula of the volume of cones. Establish a relation between the radius of smaller and the larger cone by the use of similarity of triangles. Consider some height to proceed further.
Complete step-by-step answer:
We will solve the problem with the help of following figure
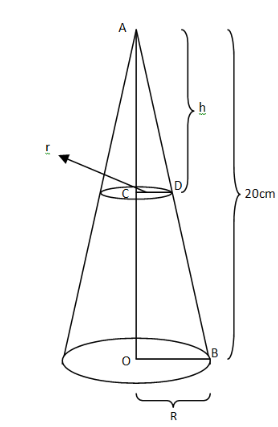
Given: Height of the cone $ = 20cm$
As shown in the figure
Let the small cone be cut off at a height $h$ from the top.
Let the radius of the big cone be $R$ and that of small cone be $r$
Let us consider the volume of big cone is ${V_1}$ and that of small cone be ${V_2}$
As we know that the volume of cone is
$V = \dfrac{1}{3}\pi {r^2}h$
Where $r = $ radius of the base of the cone
And $h = $ height of the cone
So, volume of the bigger cone
$
{V_1} = \dfrac{1}{3}\pi {R^2}h \\
= \dfrac{1}{3}\pi {R^2} \times 20 \\
= \dfrac{{20}}{3}\pi {R^2}{\text{ cu}}{\text{.cm}} \\
$
And the volume of small cone
${V_1} = \dfrac{1}{3}\pi {r^2}h$
As we know, the ratio of volume of both the cones is $\dfrac{1}{{125}}$.
$
\Rightarrow \dfrac{{{V_2}}}{{{V_1}}} = \dfrac{1}{{125}} \\
\Rightarrow \dfrac{{\dfrac{1}{3}\pi {r^2}h}}{{\dfrac{{20}}{3}\pi {R^2}}} = \dfrac{1}{{125}} \\
\Rightarrow \dfrac{{{r^2}h}}{{20{R^2}}} = \dfrac{1}{{125}} \\
$
Further manipulating the equation for substitution
$ \Rightarrow \dfrac{{{r^2}}}{{{R^2}}} \times \dfrac{h}{{20}} = \dfrac{1}{{125}}$ …………(1)
Now in $\Delta ACD\& \Delta AOB$
$
\because \angle CAD = \angle OAB\left[ {{\text{same angle}}} \right] \\
\& \angle ACD = \angle AOB\left[ {{\text{both are 9}}{{\text{0}}^0}} \right] \\
$
So $\Delta ACD\& \Delta AOB$ are similar by AA criterion
Therefore ratio of their similar sides will be equal
$
\Rightarrow \dfrac{{CD}}{{OB}} = \dfrac{{AD}}{{AB}} \\
\Rightarrow \dfrac{r}{R} = \dfrac{h}{{20}}..........(2) \\
$
Substituting the value from equation (2) to equation (1)
$
\Rightarrow {\left( {\dfrac{h}{{20}}} \right)^2} \times \dfrac{h}{{20}} = \dfrac{1}{{125}} \\
\Rightarrow {\left( {\dfrac{h}{{20}}} \right)^3} = \dfrac{1}{{125}} = {\left( {\dfrac{1}{5}} \right)^3} \\
\Rightarrow \dfrac{h}{{20}} = \dfrac{1}{5} \\
\Rightarrow h = \dfrac{{20}}{5} = 4cm \\
$
So the height above the base from where the section is made is $20cm - 4cm = 16cm$
Hence, the height of the section from the base is $16cm$
Note- In these types of geometrical questions, the figure plays a vital role in solution. So always try to start with a figure for better understanding. Just don’t look at the figure as a 3-D image, rather try to see it in 2-D as well, which helped us in finding the similarity between the triangles and the ratio of the radius of the two cones. Also remember different similarity conditions of the triangle, one of which is mentioned above.
Complete step-by-step answer:
We will solve the problem with the help of following figure
Given: Height of the cone $ = 20cm$
As shown in the figure
Let the small cone be cut off at a height $h$ from the top.
Let the radius of the big cone be $R$ and that of small cone be $r$
Let us consider the volume of big cone is ${V_1}$ and that of small cone be ${V_2}$
As we know that the volume of cone is
$V = \dfrac{1}{3}\pi {r^2}h$
Where $r = $ radius of the base of the cone
And $h = $ height of the cone
So, volume of the bigger cone
$
{V_1} = \dfrac{1}{3}\pi {R^2}h \\
= \dfrac{1}{3}\pi {R^2} \times 20 \\
= \dfrac{{20}}{3}\pi {R^2}{\text{ cu}}{\text{.cm}} \\
$
And the volume of small cone
${V_1} = \dfrac{1}{3}\pi {r^2}h$
As we know, the ratio of volume of both the cones is $\dfrac{1}{{125}}$.
$
\Rightarrow \dfrac{{{V_2}}}{{{V_1}}} = \dfrac{1}{{125}} \\
\Rightarrow \dfrac{{\dfrac{1}{3}\pi {r^2}h}}{{\dfrac{{20}}{3}\pi {R^2}}} = \dfrac{1}{{125}} \\
\Rightarrow \dfrac{{{r^2}h}}{{20{R^2}}} = \dfrac{1}{{125}} \\
$
Further manipulating the equation for substitution
$ \Rightarrow \dfrac{{{r^2}}}{{{R^2}}} \times \dfrac{h}{{20}} = \dfrac{1}{{125}}$ …………(1)
Now in $\Delta ACD\& \Delta AOB$
$
\because \angle CAD = \angle OAB\left[ {{\text{same angle}}} \right] \\
\& \angle ACD = \angle AOB\left[ {{\text{both are 9}}{{\text{0}}^0}} \right] \\
$
So $\Delta ACD\& \Delta AOB$ are similar by AA criterion
Therefore ratio of their similar sides will be equal
$
\Rightarrow \dfrac{{CD}}{{OB}} = \dfrac{{AD}}{{AB}} \\
\Rightarrow \dfrac{r}{R} = \dfrac{h}{{20}}..........(2) \\
$
Substituting the value from equation (2) to equation (1)
$
\Rightarrow {\left( {\dfrac{h}{{20}}} \right)^2} \times \dfrac{h}{{20}} = \dfrac{1}{{125}} \\
\Rightarrow {\left( {\dfrac{h}{{20}}} \right)^3} = \dfrac{1}{{125}} = {\left( {\dfrac{1}{5}} \right)^3} \\
\Rightarrow \dfrac{h}{{20}} = \dfrac{1}{5} \\
\Rightarrow h = \dfrac{{20}}{5} = 4cm \\
$
So the height above the base from where the section is made is $20cm - 4cm = 16cm$
Hence, the height of the section from the base is $16cm$
Note- In these types of geometrical questions, the figure plays a vital role in solution. So always try to start with a figure for better understanding. Just don’t look at the figure as a 3-D image, rather try to see it in 2-D as well, which helped us in finding the similarity between the triangles and the ratio of the radius of the two cones. Also remember different similarity conditions of the triangle, one of which is mentioned above.
Last updated date: 22nd Sep 2023
•
Total views: 360.9k
•
Views today: 7.60k
