Question

The hypotenuse of a right triangle is 10cm and the radius of the inscribed circle is 1cm. The perimeter of the triangle is
(A) 15 cm
(B) 22 cm
(C) 24 cm
(D) 18 cm

Answer 1

Hint: We solve this question by first assuming the other sides of the right-angled triangle as a and b. then we divide the sides into two parts and assume them as the tangents from vertices of the triangle. Then we use the property that tangents drawn from a point to the circle are equal and use it to find the relation between a and b. Then we find the perimeter of the triangle and substitute the value obtained above to find the value of the perimeter.

Complete step-by-step solution:
Let the triangle be ABC with the right angle at vertex C. Let us assume the lengths of sides BC and CA as a and b respectively.
We are given that the radius of the circle inscribed inside the triangle is 1cm.
Let us say that the point of contact of a circle with the sides AB, AC, and BC are E, F, and G.

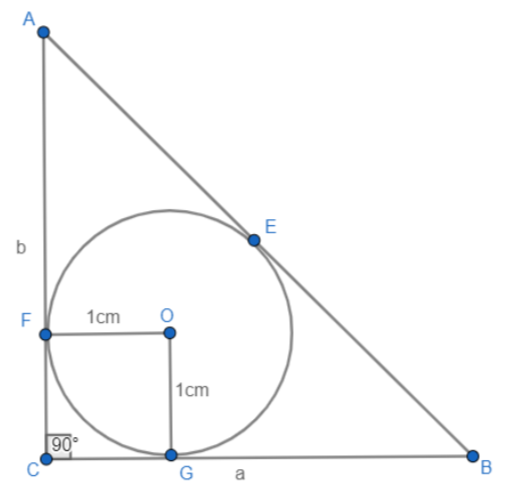
So, we have OF=OG= 1cm
As OF=GC, we get GC=1m.
We can see that CG and CF are tangents to the circle from point C.
Now let us consider the property of tangents of the circle, the lengths of tangents drawn from any point outside the circle to the circle are always equal.
Using this property, we can say that CG=CF
Similarly, AF and AE are tangents to the circle from point A and BE and BG are tangents to the circle from point B.
So, we have AF=AE and BG= BE.
We have AC = b and FC = 1cm. So, we can say that AF = b-1
We have BC = a and GC = 1cm. So, we can say that BG= a-1
As, we know that AF=AE and BG=BE, we get
$\begin{align}
  & \Rightarrow AF=AE=b-1 \\
 & \Rightarrow BG=BE=a-1 \\
\end{align}$
Now let us consider the hypotenuse of triangle.
$\begin{align}
  & \Rightarrow AB=AE+BE \\
 & \Rightarrow 10=b-1+a-1 \\
 & \Rightarrow 10=b+a-2 \\
 & \Rightarrow a+b=12 \\
\end{align}$
 Now let us consider the perimeter of the triangle
$\begin{align}
  & \Rightarrow Perimeter=AB+BC+CA \\
 & \Rightarrow Perimeter=10+a+b \\
\end{align}$
Now, let us substitute the above obtained value of (a + b) in the perimeter
$\Rightarrow Perimeter=10+12=22$
Hence perimeter of the triangle is 22cm. Hence, answer is Option B.

Note: We can also solve this problem using the properties of the triangle.
Let us consider the formula $\Delta =rs$
We are given that r=1cm. So, we have
$\begin{align}
  & \Rightarrow \Delta =s \\
 & \Rightarrow \dfrac{1}{2}ab=\dfrac{a+b+10}{2} \\
 & \Rightarrow ab=a+b+10 \\
 & \Rightarrow a+b=ab-10........\left( 1 \right) \\
\end{align}$
Now, applying the Pythagoras theorem, we have
${{a}^{2}}+{{b}^{2}}=100.........\left( 2 \right)$
Now let us consider the square of equation (1).
$\Rightarrow {{a}^{2}}+{{b}^{2}}+2ab={{\left( ab \right)}^{2}}-20ab+100$
Now let us substitute the equation (2) in the above equation.
$\begin{align}
  & \Rightarrow 100+2ab={{\left( ab \right)}^{2}}-20ab+100 \\
 & \Rightarrow {{\left( ab \right)}^{2}}-22ab=0 \\
 & \Rightarrow \left( ab \right)\left( ab-22 \right)=0 \\
\end{align}$
As a and b are lengths of sides, they are not zero, So we have
$\Rightarrow ab=22$
Now let us consider the above derived equation,
$\begin{align}
  & \Rightarrow \Delta =s \\
 & \Rightarrow \dfrac{1}{2}ab=s \\
 & \Rightarrow ab=2s \\
\end{align}$
As perimeter is equal to 2s, we have
$Perimeter=ab$
Substituting the value of ab obtained above, we get
 $Perimeter=22$
Hence answer is Option B.