
The incentre of a triangle coincides with the circumcentre, the orthocentre and the centroid in case of
[a] An isosceles triangle
[b] An equilateral triangle
[c] A right angled triangle
[d] A right angled isosceles triangle.
Answer
573.6k+ views
Hint: Recall the definition of incentre, circumcentre, orthocentre and the centroid of a triangle. Infer what happens when an altitude of the triangle is also a median. Hence determine what happens when centroid and orthocentre of the triangle coincide. Hence determine is it possible for the circumcentre to coincide too. Hence determine the nature of the triangle when the orthocentre, the circumcentre and the centroid coincide.
Complete step by step answer:
Before solving the question, we need to understand the definitions of the incentre, the centroid, the circumcentre and the orthocentre of a triangle.
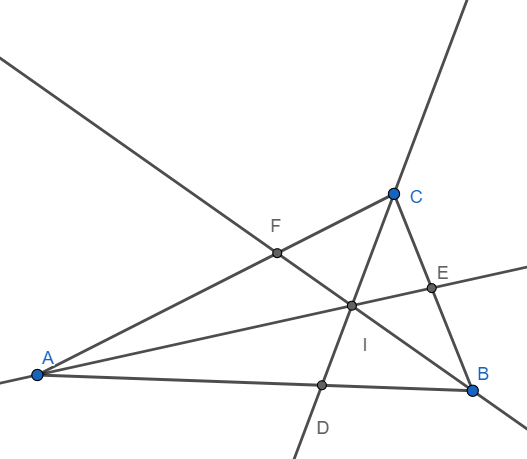
Incentre of a triangle: The point of concurrency of the angle bisectors of a triangle is known as incentre of the triangle. In the triangle ABC shown below CD, AE and BF are the angle bisectors of the triangle. Hence “I” is the incentre of the triangle.
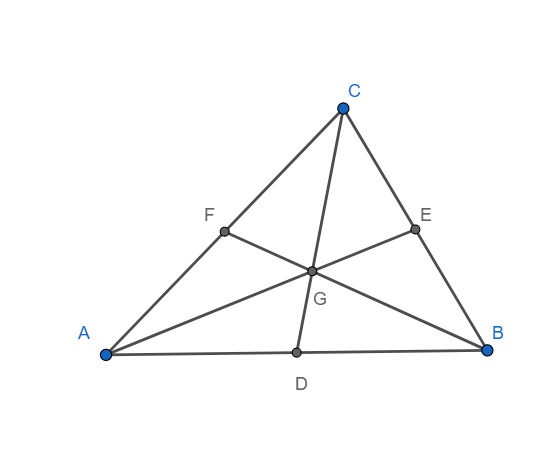
 Centroid of a triangle: The point of concurrency of the medians of a triangle is known as centroid of a triangle. In the triangle ABC shown below CD, AE and BF are the medians and hence G is the centroid of the triangle.
Centroid of a triangle: The point of concurrency of the medians of a triangle is known as centroid of a triangle. In the triangle ABC shown below CD, AE and BF are the medians and hence G is the centroid of the triangle.
Orthocentre of a triangle: The point of concurrency of the altitudes of a triangle is known as the orthocentre of the triangle. In the triangle ABC shown below CD, AE and BF are the altitudes and hence H is the orthocentre of the triangle.

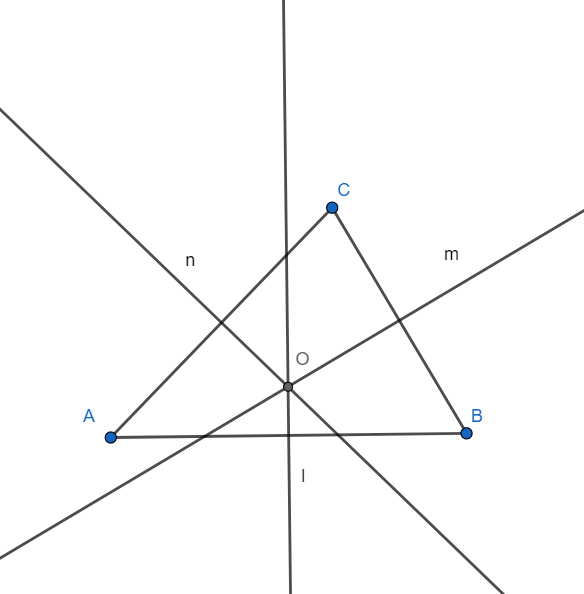
Circumcentre of a triangle: The point of intersection of the perpendicular bisector of the sides of a triangle is known as circumcentre of the triangle. Lines l, m and n are the perpendicular bisectors of the triangle of AB, BC and AC and hence O is the circumcentre of the triangle.
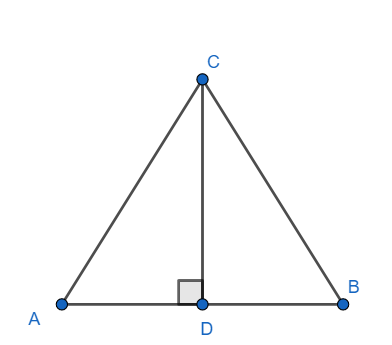
Consider a triangle ABC in which altitude AD is also the median as shown below
In triangle ADC and BCD, we have
AD = BD (Since CD is the median)
$\angle ADC=\angle BDC$(each 90)
CD = CD (Common side)
Hence by SAS congruence criterion, we have
$\Delta ADC\cong \Delta BDC$
Hence, we have AC = BC and $\angle ACD=\angle BCD$(Corresponding parts of congruent triangles).
Hence if a median of side is also the altitude of the side then the other two sides of the triangle are equal. Also the median and the altitude is a perpendicular bisector and an angle bisector to the side too.
Now suppose that the centroid of the triangle and the orthocentre coincide as shown in figure below with F as the point of coincidence of centroid and the orthocentre.
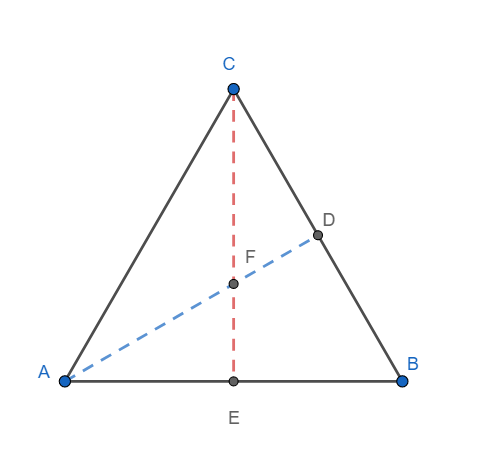
Since F is the centroid, AD is a median.
Since F is the orthocentre AD is an altitude.
Hence AD is both an altitude and a median.
Hence AC = AB (i) and AD is a perpendicular bisector and an angle bisector (Using the result derived above).
Since F is the centroid, CE is a median
Since F is the orthocentre CE is an altitude.
Hence, CE is both an altitude and a median.
Hence AC = BC (ii) and CE is a perpendicular bisector and an angle bisector (Using the result derived above)
Form equation (i) and (ii), we have AB = BC = AC, i.e. ABC is an equilateral triangle.
Also, F is the point of intersection of perpendicular bisectors and angle bisectors and hence F is the circumcentre and incentre too.
Hence if in a triangle the incentre, the orthocentre, the circumcentre and the centroid coincide then the triangle is an equilateral triangle.
Note: Remember the above result. Converse of the result is also true, i.e. in an equilateral triangle, the centroid, the circumcentre and the orthocentre coincide with each other. There’s a possibility that students might not understand the question clearly and mark the right angled triangle as the correct answer. But, for this type of question, it is always advised to define the terms, draw figures for all triangles given in the option and check if circumcentre, orthocentre and centroid coincide with the incentre or not.
Complete step by step answer:
Before solving the question, we need to understand the definitions of the incentre, the centroid, the circumcentre and the orthocentre of a triangle.
Incentre of a triangle: The point of concurrency of the angle bisectors of a triangle is known as incentre of the triangle. In the triangle ABC shown below CD, AE and BF are the angle bisectors of the triangle. Hence “I” is the incentre of the triangle.


Orthocentre of a triangle: The point of concurrency of the altitudes of a triangle is known as the orthocentre of the triangle. In the triangle ABC shown below CD, AE and BF are the altitudes and hence H is the orthocentre of the triangle.

Circumcentre of a triangle: The point of intersection of the perpendicular bisector of the sides of a triangle is known as circumcentre of the triangle. Lines l, m and n are the perpendicular bisectors of the triangle of AB, BC and AC and hence O is the circumcentre of the triangle.

Consider a triangle ABC in which altitude AD is also the median as shown below

In triangle ADC and BCD, we have
AD = BD (Since CD is the median)
$\angle ADC=\angle BDC$(each 90)
CD = CD (Common side)
Hence by SAS congruence criterion, we have
$\Delta ADC\cong \Delta BDC$
Hence, we have AC = BC and $\angle ACD=\angle BCD$(Corresponding parts of congruent triangles).
Hence if a median of side is also the altitude of the side then the other two sides of the triangle are equal. Also the median and the altitude is a perpendicular bisector and an angle bisector to the side too.
Now suppose that the centroid of the triangle and the orthocentre coincide as shown in figure below with F as the point of coincidence of centroid and the orthocentre.

Since F is the centroid, AD is a median.
Since F is the orthocentre AD is an altitude.
Hence AD is both an altitude and a median.
Hence AC = AB (i) and AD is a perpendicular bisector and an angle bisector (Using the result derived above).
Since F is the centroid, CE is a median
Since F is the orthocentre CE is an altitude.
Hence, CE is both an altitude and a median.
Hence AC = BC (ii) and CE is a perpendicular bisector and an angle bisector (Using the result derived above)
Form equation (i) and (ii), we have AB = BC = AC, i.e. ABC is an equilateral triangle.
Also, F is the point of intersection of perpendicular bisectors and angle bisectors and hence F is the circumcentre and incentre too.
Hence if in a triangle the incentre, the orthocentre, the circumcentre and the centroid coincide then the triangle is an equilateral triangle.
Note: Remember the above result. Converse of the result is also true, i.e. in an equilateral triangle, the centroid, the circumcentre and the orthocentre coincide with each other. There’s a possibility that students might not understand the question clearly and mark the right angled triangle as the correct answer. But, for this type of question, it is always advised to define the terms, draw figures for all triangles given in the option and check if circumcentre, orthocentre and centroid coincide with the incentre or not.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
The shortest day of the year in India

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




