Question

The incentre of the triangle with vertices \[\left( 1,\sqrt{3} \right),\left( 0,0 \right)\] and \[\left( 2,0 \right)\]is
\[\left( 1,\dfrac{\sqrt{3}}{2} \right)\]
\[\left( \dfrac{2}{3},\dfrac{1}{\sqrt{3}} \right)\]
\[\left( \dfrac{2}{3},\dfrac{\sqrt{3}}{2} \right)\]
\[\left( 1,\dfrac{1}{\sqrt{3}} \right)\]
.

Answer 1

Hint:To solve the question, we have to analyse the type of the given triangle which will result in the given triangle being an equilateral triangle. To solve further, apply the properties of the equilateral triangle, which states that the centroid and incentre of equilateral triangle coincide. To solve further, calculate the centroid of the given triangle to find the value of the incentre.

Complete Step-by-step answer:
Let the given triangle be \[\Delta ABC\]with vertices A, B, C as\[\left( 1,\sqrt{3} \right),\left( 0,0 \right)\left( 2,0 \right)\] respectively.
We know the formula for the distance between two points \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)\]is given by \[\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}\]
Thus, by applying the formula for the given values we get
The length of side AB =\[\sqrt{{{\left( 1-0 \right)}^{2}}+{{\left( \sqrt{3}-0 \right)}^{2}}}=\sqrt{{{1}^{2}}+{{\left( \sqrt{3} \right)}^{2}}}=\sqrt{1+3}=\sqrt{4}=2\]
\[\Rightarrow \]AB = 2 units.
The length of side BC =\[\sqrt{{{\left( 0-2 \right)}^{2}}+{{\left( 0-0 \right)}^{2}}}=\sqrt{{{\left( -2 \right)}^{2}}+{{\left( 0 \right)}^{2}}}=\sqrt{4+0}=\sqrt{4}=2\]
\[\Rightarrow \] BC = 2 units.
The length of side CA =\[\sqrt{{{\left( 1-2 \right)}^{2}}+{{\left( \sqrt{3}-0 \right)}^{2}}}=\sqrt{{{\left( -1 \right)}^{2}}+{{\left( \sqrt{3} \right)}^{2}}}=\sqrt{1+3}=\sqrt{4}=2\]
\[\Rightarrow \] CA = 2 units.
Thus, AB = BC = CA
We know that a triangle is an equilateral triangle when all the three sides of the triangle are equal.
Thus, we conclude that \[\Delta ABC\]is an equilateral triangle, as shown below:

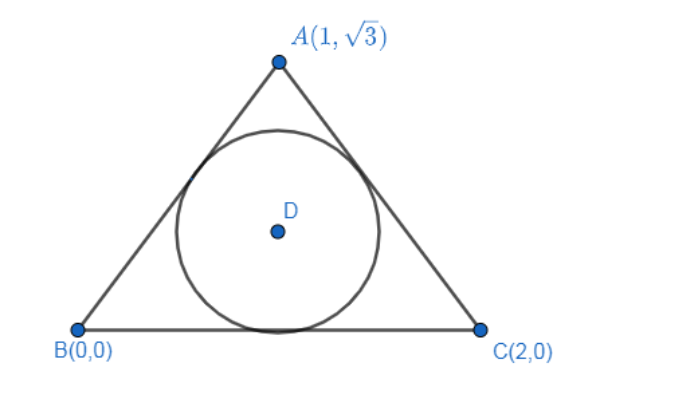
Here D is the centroid or incentre of the given triangle.

We know that the formula for centroid of a triangle is equal to
\[\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)\] where \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)\left( {{x}_{3}},{{y}_{3}} \right)\] are vertices of a triangle.
By substituting the values in the above formula, we get
The centroid of \[\Delta ABC\]is equal to \[\left( \dfrac{1+0+2}{3},\dfrac{\sqrt{3}+0+0}{3} \right)=\left( \dfrac{3}{3},\dfrac{\sqrt{3}}{3} \right)=\left( 1,\dfrac{\sqrt{3}}{{{\left( \sqrt{3} \right)}^{2}}} \right)=\left( 1,\dfrac{1}{\sqrt{3}} \right)\]
Thus, the centroid of \[\Delta ABC\]is equal to \[\left( 1,\dfrac{1}{\sqrt{3}} \right)\]
We know that in an equilateral triangle centroid and incentre of the triangle coincidence.
Thus, the incentre of the triangle is equal to \[\left( 1,\dfrac{1}{\sqrt{3}} \right)\]
Hence, option (d) is the right choice.

Note:The possibility of mistake can be not analysing the type of the given triangle which eases the procedure of solving. The other possibility of mistake can be not applying the properties of the analysed type of triangle. The alternative way of solving the question is by using the direct formula for incentre which is equal to \[\left( \dfrac{a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}}}{a+b+c},\dfrac{a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}}}{a+b+c} \right)\]where a, b, c are the side lengths and \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)\left( {{x}_{3}},{{y}_{3}} \right)\] are vertices of the given triangle.