Question

The ionic radii of Cs and CI are 0.165 nm and 0.181 nm respectively. Their atomic weights are 133 amu?
A. the lattice parameter (a) is 0.4 nm
B. the lattice parameter cannot be determined from this data
C. the density of CsCI is \[4.31 \times {10^3}kg{m^3}\]
D. CCI has an fcc structure based on the given information

Answer 1

Hint: To solve this problem, we must first understand the type of unit cell present in the structure of CsCI. Then we can calculate the lattice parameter of this unit cell and by relation, correspond to the value of density of the unit cell of CsCI.

Complete step by step answer:

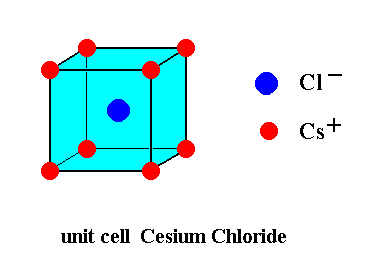
Now CsCI has a lattice where the chlorine is at the eight corners of the cubic unit cell. And the Cs ion is at the body center of the unit cell. But it is not the body-centered unit cell because in the case of Body-centered unit cell the same atoms are at the corners and the middle of the unit cell.
The lattice parameter of CsCI is,
 \[2({r_ + } + {r_ - }) = a\sqrt 3 \] , now the ionic radii of Cs and CI are 0.165 nm and 0.181 nm respectively.
So, the value of the lattice parameter (a) is,
 \[
  \Rightarrow 2(0.165 + 0.181) = a\sqrt 3 \\
  \Rightarrow 2 \times (0.346) = a\sqrt 3 \\
  \Rightarrow 0.692 = a\sqrt 3 \\
  \Rightarrow \dfrac{{0.692}}{{\sqrt 3 }} = a \\
  \Rightarrow 0.489 = a \\
 \]
So, the lattice parameter (a) is 0.4 nm, option A is correct.
Now the formula for density,
 \[\rho = \dfrac{{ZM}}{{{N_A}{{(a)}^3}}}\]
Molecular mass M is, 133+35.5=168.5. The Z value is 1. Now the density is,
 \[
  \rho = \dfrac{{ZM}}{{{N_A}{{(a)}^3}}} \\
   = \dfrac{{1 \times (133 + 35.5)}}{{6.02 \times {{10}^{23}} \times {{(4 \times {{10}^{ - 10}})}^3}}} \\
   = \dfrac{{168.5}}{{6.02 \times {{10}^{23}} \times {{(4 \times {{10}^{ - 10}})}^3}}} \\
   = 4.37 \times \;{10^3}kg{m^3} \\
 \]

So, the density of CsCI is \[4.31 \times {10^3}kg{m^3}\] option C is correct.

Note:The classification of various structures can be done by finding the radius ratio of the cation and anion. Depending upon the range of the radius ratio, we can classify the structures.
The radius ratio (also known as the radius ratio rule), is the ratio of the ionic radius of the cation to the ionic radius of the anion in a cation-anion compound.
The radius ratio of cation and anion is given by \[\dfrac{{{r_{cation}}}}{{{r_{anion}}}}\] .
Here, the ionic radii of Cs and CI are 0.165 nm and 0.181 nm respectively. so, the value of radius ratio of CsCI is,
 \[
  \dfrac{{{r_{cation}}}}{{{r_{anion}}}} \\
   = \dfrac{{0.165}}{{0.181}} \\
 \]
=0.911
So, the coordination number is 8.