Question

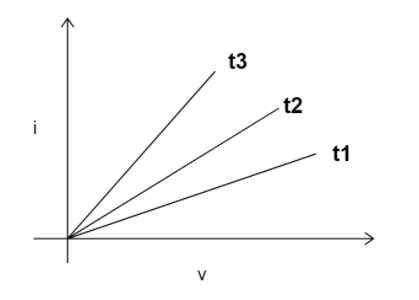
The I-V graph for a resistance at temperature${t_1}$, ${t_2}$, ${t_3}$ is shown in the figure. The highest temperature is:
A. ${t_1}$
B. ${t_2}$
C. ${t_3}$
D. ${t_1} = {t_2} = {t_3}$

Answer 1

Hint: In case of resistances, with increase in temperature, the resistance of the conductor also increases. This implies that resistance is directly proportional to temperature. Thus at the highest temperature, resistance is also highest.

Complete step by step answer:
The above graph is a v-I graph. We know, according to the ohm’s law, that in case of conductors, the current flowing through the conductor is directly proportional to potential difference across its two ends provided physical factors like pressure, temperature remain constant.
Thus, mathematically we can say:
$I \propto V$
Where,
$I = $Current through the conductor.
$V = $ Voltage across the ends
The constant of proportionality, in the equation, is resistance, denoted by the letter$R$.
Thus the equation becomes:
$V = IR$
We know, in case of conductors, the ohm’s law graph comes to be a straight line.
As shown above, the x-axis in the graph represents Voltage and Y axis represents Current.
Thus, consider the equation of straight line: $Y = mX$
Comparing, the equation of straight line from the equation of ohm’s law, we obtain:
$R = \dfrac{1}{m}$
Where, $m$ is the slope of the graph.
Thus, we can infer, the steeper the slope, lesser will be the value of resistance.
We can see that steepness of the slope decreases as:
${m_1} < {m_2} < {m_3}$
Where, ${m_1}$, ${m_2}$, ${m_3}$ are the slopes of the respective curves.
Thus, we can say, resistance decreases in the order, ${R_1} > {R_2} > {R_3}$.
Since, temperature is directly proportional to resistance, temperature also decreases in the order:
${t_1} > {t_2} > {t_3}$.
Thus, ${t_1}$is the highest temperature.

Hence, the correct answer is option (A).

Note: We know that resistance of the conductor is also proportional to resistivity of the conductor. Therefore. With increase in temperature, resistivity of the conductor also increases. . Since resistance of the conductor is proportional to the resistivity of it, we can say that resistance also increases.