
The largest possible sphere is carved out of a cube of side 7 cm. Find the volume of wood left.
Answer
520.5k+ views
Hint: This is a problem of volumes. One should know the formula for the volume of cube and sphere. They are given by-
To solve this problem, we will find the volume of the cube and largest sphere, then subtract them.
Complete step-by-step answer:
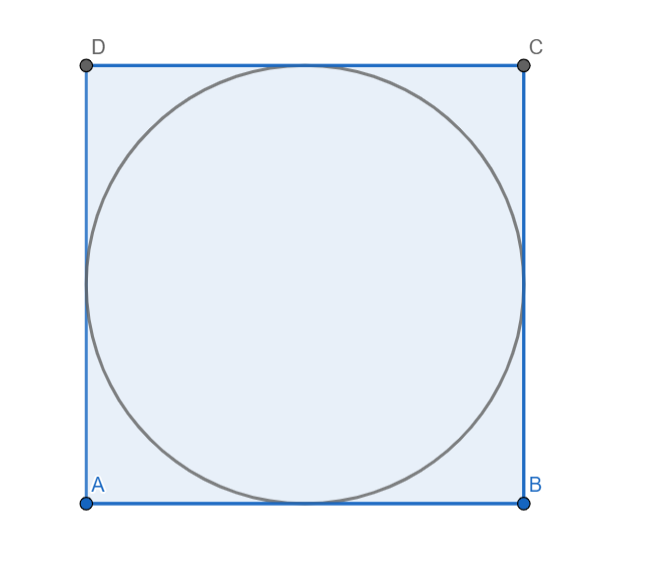
This is a front view of the figure. We can clearly see that the radius of the sphere is half the side of the cube, so radius of the sphere is r = 3.5 cm.
Volume of the cube = (side)3 = 73 = 343 cm3
Volume of sphere =
The volume of wood left = 343 -179.66 = 163.33 cm3
This is the required answer.
Note: To solve such problems, making a diagram is necessary and helpful, because using the diagram, we easily found the radius of the square. Also, do not forget to write the units in the answer.
To solve this problem, we will find the volume of the cube and largest sphere, then subtract them.
Complete step-by-step answer:

This is a front view of the figure. We can clearly see that the radius of the sphere is half the side of the cube, so radius of the sphere is r = 3.5 cm.
Volume of the cube = (side)3 = 73 = 343 cm3
Volume of sphere =
The volume of wood left = 343 -179.66 = 163.33 cm3
This is the required answer.
Note: To solve such problems, making a diagram is necessary and helpful, because using the diagram, we easily found the radius of the square. Also, do not forget to write the units in the answer.
Latest Vedantu courses for you
Grade 7 | CBSE | SCHOOL | English
Vedantu 7 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹45,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Where did Netaji set up the INA headquarters A Yangon class 10 social studies CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility




