Question

The lattice energy of NaCl is 788kJ/mol. This means that 788kJ of energy is required.
(A) to separate one mole of NaCl into one mole $N{{a}_{(g)}}$ and one mole of $C{{l}_{(g)}}$ to infinite distance.
(B) to separate one mole of solid NaCl into one mole of $N{{a}^{+}}_{(g)}$ and one mole of $C{{l}_{(g)}}$ to infinite distance.
(C) to convert one mole of solid NaCl into one mole of gaseous NaCl.
(D) to convert one mole of gaseous NaCl into one mole of solid NaCl.

Answer 1

Hint: Lattice energy is the energy required to break apart an ionic solid and convert its component atoms into gaseous ions. Hence the value of lattice energy is always positive and endothermic.

Complete step by step answer:
Since it is impossible to determine the lattice energy directly by experiment, but can determine the indirect method by constructing an enthalpy or energy diagram is called a Born-Haber cycle.
\[\begin{align}
  & NaCl(s)\to N{{a}^{+}}(g)+C{{l}^{-}}(g); \\
 & {{\Delta }_{lattice}}{{H}^{-}}=+788kJmo{{l}^{-1}} \\
\end{align}\]

Let us know the value of lattice energy from the Born-Haber cycle,
Step-1: sublimation of sodium metal
$Na(s)\to Na(g);{{\Delta }_{sub}}{{H}^{\Theta }}=108.4kJmo{{l}^{-1}}$

Step-2: the ionization of sodium atoms, ionization enthalpy will be
$Na(g)\to N{{a}^{+}}(g)+{{e}^{-1}}(g);{{\Delta }_{i}}{{H}^{\Theta }}=496kJmo{{l}^{-1}}$

Step-3: the dissociation of chlorine, the reaction enthalpy is half of the bond dissociation enthalpy.
$\dfrac{1}{2}C{{l}_{2}}(g)\to Cl(g);\dfrac{1}{2}{{\Delta }_{bond}}{{H}^{\Theta }}=121kJmo{{l}^{-1}}$

Step-4: electron gain enthalpy, electron affinity enthalpy value,
$Cl(g)+{{e}^{-1}}(g)\to C{{l}^{-}}(g);{{\Delta }_{a}}{{H}^{\Theta }}=-348.6kJmo{{l}^{-1}}$

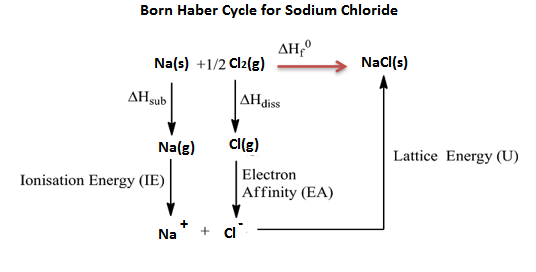
The sequence of steps shown in the above enthalpy diagram of NaCl is known as the Born-Haber cycle. The importance of the cycle is that the sum of enthalpy changes round a cycle is zero.
From the above lattice enthalpy diagram, the energy +788kJ/mol is required to separate one mole of solid NaCl into one mole of $N{{a}^{+}}_{(g)}$ and one mole of $C{{l}_{(g)}}$ to infinite distance.
So, the correct answer is “Option B”.

Note: Lattice energy is used to explain the stability of ionic solids. Some might expect such an ordered structure to be less stable because the entropy of the system would be low. A lot of energy is released as the oppositely charged ions interact. It is that causes ionic solids to have such high melting and boiling points. Some require such high temperatures that they decompose before reaching the melting point or boiling point.