Question

The least number of non-collinear points required to determine a plane is:
(a) One
(b) Two
(c) Three
(d) Infinite

Answer 1

Hint: In this question, we use the concept of three dimensions (3-D). We know planes are three dimensional figures so we use non- collinear points and observe how many non- collinear points are required to draw a plane.

Complete step-by-step solution -

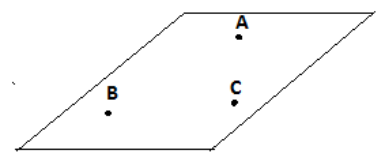
Now, we have to find minimum number points (non-collinear) required to determine a plane and we have to use non-collinear points. Non- collinear means that two or more points do not lie on the same line.
If we take only one point so we cannot make any type of figure.
If we take two points so we can make only a line because the line is two dimensional, it requires only two points.
Since, at-least two points determine a line.
Now, if we add one more point, it will become a plane because the line is two dimensional figures and we add one more point so it becomes three dimensional figures.
Thus, at-least three points are required to determine a plane.
So, the correct option is (c).

Note: In such types of problems we have to use geometrical interpretation. We have to take one by one point and observe which type of figure is made. We know a line is two dimensional and is made up of two points then if we add one more point then three dimensional figures create and we know planes are three dimensional figures.