Question

The length and breadth of a rectangular field are 120 m and 80 m respectively. Inside the field, a park of 12 m width is made around the field. The area of the part is?
A.3224 m\[^2\]
B.7344 m\[^2\]
C.2256 m\[^2\]
D.4224 m\[^2\]

Answer 1

Hint: First we will use the formula of area of a rectangular field,\[lb\], where \[l\] is the length and \[b\] is the breadth. After that, we will calculate the area of the field apart from the park and then find the difference to calculate the required value.

Complete step-by-step answer:
We are given that the length and breadth of a rectangular field are 120 m and 80 m respectively and inside the field, a park of 12 m width is made around the field.
Let us assume that the ABEF is the park and DOPC is the rectangular field.

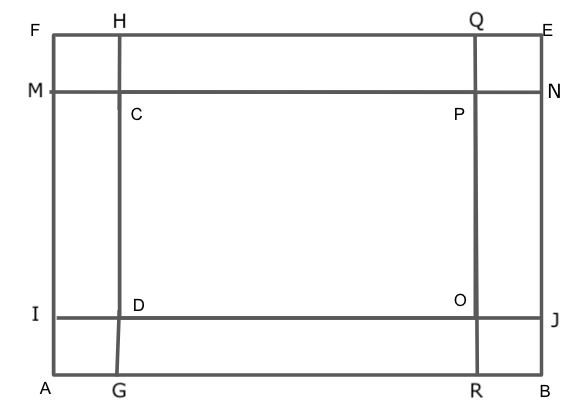
So, we have the length AB and EF is 120 m and the length AF and BE is 80 m.
Since we are given that the width of the park is 12 m, then we will have the value of DG, PN, QP, MC, DI, AI, EN, HC and MF is 12 m.
Now we will compute the dimensions of the new field.
We know that the lengths of DO and PC are equal and the lengths of OP and CD are equal.
Computing the length of DO by substituting the value of AB and DI in\[AB - 2DI\], we get
\[
   \Rightarrow 120 - 2\left( {12} \right) \\
   \Rightarrow 120 - 24 \\
   \Rightarrow 96{\text{ m}} \\
 \]
Thus, the length of DO and PC is 96 m.
Computing the length of OP by substituting the value of AF and AI in\[AF - 2AI\], we get
\[
   \Rightarrow 80 - 2\left( {12} \right) \\
   \Rightarrow 80 - 24 \\
   \Rightarrow 56{\text{ m}} \\
 \]
Thus, the length of OP and AF is 56 m.
We know that the formula of the area of a rectangular field,\[lb\], where \[l\] is the length and \[b\] is the breadth.
Calculating the area of original park ABEF, we get
\[
   \Rightarrow 120 \times 80 \\
   \Rightarrow 9600{\text{ }}{{\text{m}}^2} \\
 \]
Calculating the area of new park DOPC, we get
\[
   \Rightarrow 96 \times 56 \\
   \Rightarrow 5376{\text{ }}{{\text{m}}^2} \\
 \]
Finding the area of the park by subtracting the area of DOPC from ABEF, we get
\[
   \Rightarrow \left( {9600 - 5376} \right){\text{ }}{{\text{m}}^2} \\
   \Rightarrow 4224{\text{ }}{{\text{m}}^2} \\
 \]

Hence, option D is correct.

Note: In solving these types of questions, students should remember that the area of any shape is the product of the length of all its sides. And there are four sides in a rectangle out of which opposite sides are equal and adjacent sides are different. And the adjacent sides of the rectangle are known as length and breadth. So students should know that the width is also a breadth. So, the formula will be the same as is given for the area of a rectangular.