Question

The length, breadth and height of a room are 8 m 50 cm, 6 m 25 cm and 4 m 75 cm respectively. Find the length of the longest rod that can measure the dimensions of the room exactly.

Answer 1

Hint: Suppose we have a rod of length 50 cm. It cannot measure a length of 25 cm. Now, a rod of length 25 cm can measure all the lengths of the room, but is it really the longest such rod possible?
The longest length of the rod will be the largest number which can divide all of them, or in other words, it will be the HCF of the given values.

Complete step-by-step answer:

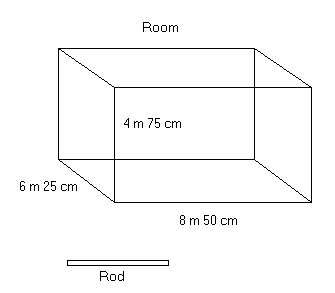
Let us convert the given values in the same unit, say cm. We know that there are 100 cm in 1 m.
Therefore, Length = 850 cm, Breadth = 625 cm and Height = 475 cm.
Factoring into prime numbers, the values are:
850 = 2 × $5^2$ × 17
625 = $5^4$
475 = $5^2$ × 19
The HCF of these numbers is $5^2$ = 25.
Therefore, the length of the longest rod that can measure all the three sides is 25 cm.

Note: The HCF is also called GCD (Greatest Common Divisor). In order to find the HCF of decimal numbers (fractions), first multiply all of them by the same number x so that they become integers. Finally, divide the HCF of these integers by the same x.
The notation (a, b) is sometimes used for "GCD / HCF of a and b".
It is useful to know that a factor of two numbers is also a factor of their sum or difference, a fact that is rigorously used in Euclid's algorithm to find the HCF of two numbers.
Euclid's Division Algorithm states that the GCD (a, b), of two numbers a and b, can always be written in the form: (a, b) = am + bn.
Euclid’s Division Lemma: If a and b are positive integers such that a = bq + r, then every common divisor of a and b is a common divisor of b and r, and vice-versa.