
The length of the transverse common tangent of the circles
(a)
(b)3 units
(c)9 units
(d)
Answer
531k+ views
Hint: By using the general equation of circle, we find the coordinates of center and radius for the given circles. After that we determine the distance between two circles. By using all these values, we can evaluate the length of the transverse common tangent.
Complete step-by-step answer:
From the general equation of circle
Now, using the general equation we can find the coordinates of center and radius for the equation of circle given in the problem statement.
The equation of first circle, let E1:
So, the coordinate of the first circle is:
Now, the equation of second circle, let E2:
So, the coordinate of this circle is:
So, diagrammatically the condition of tangent can be shown as:
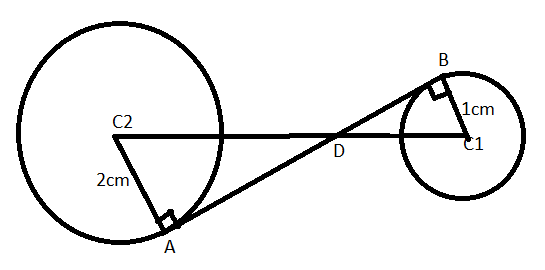
Now, we have to find the distance between two circles i.e. d,
By using the distance formula between two points (a, b) and (c, d):
So, the distance between (1, -2) and (-2, 1) will be:
So, distance between the circles is greater than the sum of both the radii of circle,
Therefore, E1 and E2 are not intersecting each other.
The length of transverse common tangent can be expressed as:
By putting values in the above expression, we get
Hence, the length of the transverse common tangent is 3units.
Therefore, option (b) is correct.
Note: The key concept for solving this question is the knowledge of the general equation of a circle and its various associated parameters. It is a direct question so by putting the values we get the desired answer. This knowledge is helpful in solving complex problems.
Complete step-by-step answer:
From the general equation of circle
Now, using the general equation we can find the coordinates of center and radius for the equation of circle given in the problem statement.
The equation of first circle, let E1:
So, the coordinate of the first circle is:
Now, the equation of second circle, let E2:
So, the coordinate of this circle is:
So, diagrammatically the condition of tangent can be shown as:

Now, we have to find the distance between two circles i.e. d,
By using the distance formula between two points (a, b) and (c, d):
So, the distance between (1, -2) and (-2, 1) will be:
So, distance between the circles is greater than the sum of both the radii of circle,
Therefore, E1 and E2 are not intersecting each other.
The length of transverse common tangent can be expressed as:
By putting values in the above expression, we get
Hence, the length of the transverse common tangent is 3units.
Therefore, option (b) is correct.
Note: The key concept for solving this question is the knowledge of the general equation of a circle and its various associated parameters. It is a direct question so by putting the values we get the desired answer. This knowledge is helpful in solving complex problems.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

How do you prove that the diagonals of a rectangle class 10 maths CBSE




