Question

The length of the unit cell edge of a body-centred cubic metal crystal is 352 pm. Calculate the radius (in pm) of an atom of the metal
A.152.4
B.15.2
C.14.2
D.182.0

Answer 1

Hint:
In the BCC structure, we have atoms on all vertices as well as one atom is present in the centre of the cube. This means that there are a total of 2 atoms in the entire BCC unit cell.
Formula Used: \[c = \dfrac{{a\sqrt 3 }}{4}\]

Complete step by step answer:
-Let us first understand how we derive the formula for calculating the atomic radius for an atom present in a body-centred cubic metal crystal.
- In a body centred cubic structure, there are atoms present on all 8 vertices of the cube and one atom is present in the centre of the cube. As shown in the figure above, let us consider the length of the side of the cube to be ‘a’ units, the length of the diagonal of the cube to be ‘b’ units and the radius of the atom to be equal to ‘c’ units.
For calculating the value of ‘b’, let us consider the \[\vartriangle EFD\].
In \[\vartriangle EFD\], EF = ED = ‘a’ units and \[\angle FED = 90^\circ \]. Hence \[\vartriangle EFD\]is a right-angled triangle.
Applying Pythagoras theorem, we get,
\[{(EF)^2} + {(ED)^2} = {(FD)^2}\]
\[\therefore {(a)^2} + {(a)^2} = {(b)^2}\]
\[\therefore 2{(a)^2} = {(b)^2}\]
\[\therefore b = a\sqrt 2 \]… (1)

For calculating the value of ‘c’, let us consider the \[\vartriangle AFD\].
In \[\vartriangle AFD\], AD = FD = ‘b’ units and \[\angle FED = 90^\circ \]. Hence \[\vartriangle AFD\]is a right-angled triangle.
Applying Pythagoras theorem, we get,
\[{(AD)^2} + {(FD)^2} = {(FA)^2}\]
\[\therefore {(a)^2} + {(b)^2} = {(FA)^2}\]
\[\therefore {(a)^2} + {(a\sqrt 2 )^2} = {(FA)^2}\]
\[\therefore F{A^2} = {a^2} + 2{a^2}\]
\[\therefore FA = a\sqrt 3 \]… (2)

We can see from the diagram that only a quarter of an atom is inside the cube at the vertices. And, along the diagonal FA, we have 2 quarter atoms and one full atom. This can be represented as:

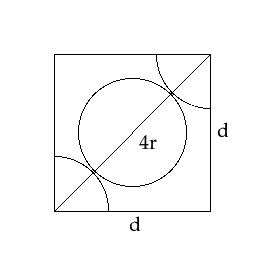
Hence, there are 4 radii along the diagonal of the cube, i.e. FA = 4c … (3)

From equations (2) and (3) we get,
\[\therefore 4c = a\sqrt 3 \]
\[\therefore c = \dfrac{{a\sqrt 3 }}{4}\]
Now, getting back to question, we can calculate the radius of the atom in the given body-centred cubic metal crystal. Since the edge length is 352 pm,
Hence, radius = c \[ = \dfrac{{352\sqrt 3 }}{4}\]
Hence, radius = c = 152.4 pm

Hence, Option A is the correct option.

Note:
In order to understand the number of neighbours around each particle in a cubic lattice, we must understand a concept known as Coordination number.The coordination number for the various types of cubic arrangements are as follows:
Simple cubic lattice: 6
Body centred cubic lattice: 8
Face centred cubic lattice: 12