Question

The lever for which the mechanical advantage is less than ${\text{ }}1{\text{ }}$ has:
A) Fulcrum at midpoint between load and effort
B) Load between effort and fulcrum
C) Effort between fulcrum and load
D) Load and effort acting at the same point

Answer 1

Hint: The measure of force amplification is obtained by using a tool, a machine, or any mechanical device. The best example of mechanical advantage is a level. A movable bar that pivots on a fulcrum positioned across a fixed point is called a lever. The increase or decrease in force without considering friction is given by mechanical advantage.

Complete step by step solution:
The lever pivots on the fulcrum. It operates by applying forces at different distances from the fulcrum.

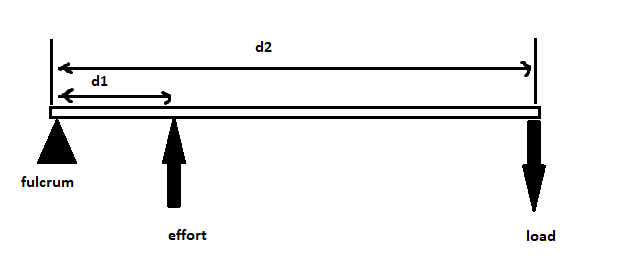
In this case, we consider the distance mechanical advantage. Distance mechanical advantage is given by the ratio of the distance moved by the load to the distance moved by the effort. If we take the distance moved by the load to be the output distance and the load moved by the effort to be the input distance, then the mechanical advantage is given by,
${\text{mechanical advantage = }}\dfrac{{{\text{output distance}}}}{{{\text{input distance}}}} = \dfrac{{{\text{load distance}}}}{{{\text{effort distance}}}}$
The mechanical advantage of less than one means that the effort distance is greater than the load distance.
Therefore, the meaning of mechanical advantage less than one is that the effort lies between the load and the fulcrum.

The answer is Option (C): Effort between fulcrum and load.

Note: In mechanical advantage, the distance direction is not considered. The distance will not be changed by friction. The mechanical advantage will be greater than one, the effort will move farther than the load. When mechanical advantage is less than one, the effort moves less than the load. In a first-class lever, the fulcrum is between the effort and lever. In a second class lever, the load is between the fulcrum and effort. In a third-class lever, the effort is between the load and fulcrum.