
The line joining the points
Answer
529.5k+ views
Hint: - Here, we use bisector formulas to find midpoints.
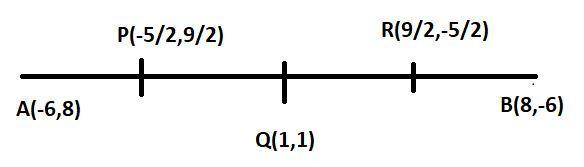
Let
So coordinates of
Similarly
So coordinates of
And now
So coordinates of
The points which divide the line in four equal parts are
Note:-Whenever we face such types of questions it is better to denote the coordinate by letter and then bisect the first line and after that bisect that line. Which are made by the bisector of the first line.
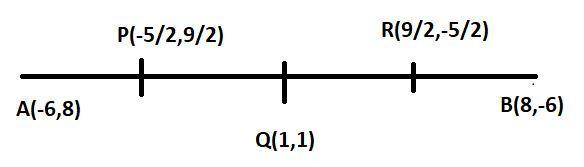
Let
So coordinates of
Similarly
So coordinates of
And now
So coordinates of
The points which divide the line in four equal parts are
Note:-Whenever we face such types of questions it is better to denote the coordinate by letter and then bisect the first line and after that bisect that line. Which are made by the bisector of the first line.
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹31,500 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Why is steel more elastic than rubber class 11 physics CBSE

Explain why a There is no atmosphere on the moon b class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE




