Question

The longest chord of the circle is a ________ of the circle.
(a) Diameter
(b) Radius
(c) Arc
(d) None of the above

Answer 1

Hint: First of all draw a circle and try to recollect all its parts like diameter, chord, radius, arc, sector, segment, etc. Now draw the longest chord possible and see to which part of the circle it resembles, among the diameter, radius, arc, etc.

Complete step-by-step answer:
In this question, we have to find the longest chord of the circle. Let us see what circle is and its different parts. A circle is basically a shape consisting of all points in a plane that are at a given distance from a given point, the center.

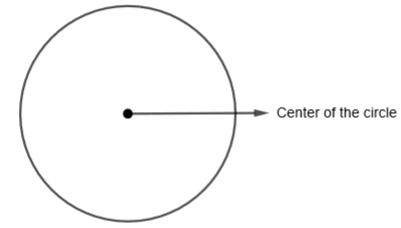
Now, let us see the different parts of the circle.
1. Radius: Radius is the distance from the center of the circle to its outer rim. AB is the radius as shown in the figure.

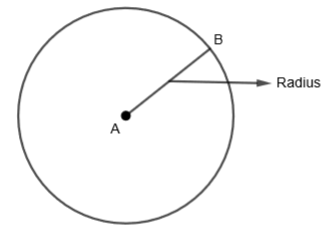
2. Chord: Chord is the line segment whose endpoints are on a circle. AB is chord as shown in the figure.

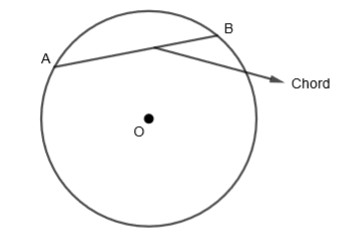
3. Diameter: Diameter is a chord that passes through the center of the circle. The length of the diameter is two times the length of the radius. AB is the diameter as shown in the figure.

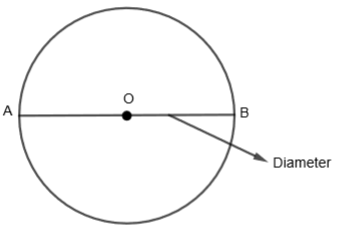
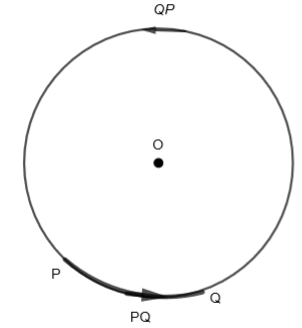
4. Arc: A continuous part of the circumference of the circle is an arc. PQ is an arc as shown in the figure. Here PQ is the minor arc and QP is the major arc.

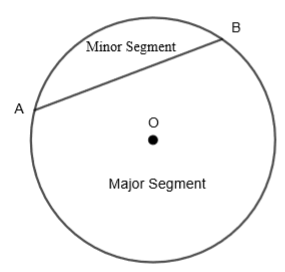
5. Segment: A chord divides the circle into parts and these two parts are called as segments of the circle.

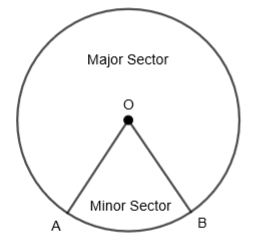
6. Sector: It is the region that lies between an arc and two radii joining the extremists of the arc and the center. OAB is the sector as shown in the figure.

Now, let us consider our question. Let us draw a circle with center O and AB as its chord.

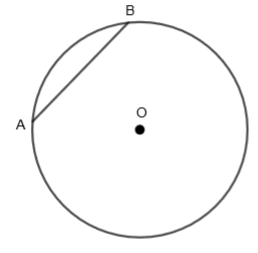
From point A, let us draw a line segment through the center that is the diameter AD. Also, join B to O.

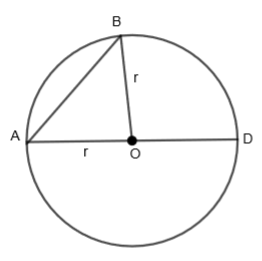
We know that the sum of two sides of the triangle is always greater than the third side. By using this in triangle AOB of the above circle, we get,
AO + OB > AB
We know that AO = OB = radius of the circle = r. So, we get,
r + r > AB
2r > AB
We know that the diameter (d) of the circle is twice the radius. So, we get,
(diameter) d > AB
From the above expression, we can conclude that for any chord that is not a diameter will be smaller than the diameter and we know that chord when passes through the center of the circle become the diameter of the circle. Hence, we can conclude that the longest chord of the circle is a diameter of the circle.
Hence, option (a) is the right answer.

Note: In this question, without the proof also, students can observe the result by drawing different chords in the circle and they will observe that the length of all the chords that do not pass from the center would be lesser than the chord which would pass the center that is the diameter. Students must know that, for the line segment to be the chord of the circle, it only has to join two points on the circumference of the circle and no other constraints are there. So, we can say that every diameter is the chord of the circle but every chord is not the diameter of the circle.