
What will be the maximum number of rectangular components into which a vector can be split in its own plane?
Answer
494.1k+ views
Hint: The rectangular components of the vector are the parts of a vector into which a vector gets resolved. Basically, these are in horizontal and vertical directions. The rectangular components will be perpendicular to each other also. Hope these all may help you to solve this question.
Complete step-by-step solution:
In a planar condition or a two-dimensional configuration, we will be moving either in a horizontal direction or vertical direction or both can also be possible. Let us assume a situation for example. Suppose you are going upstairs. When we move or go upstairs we will be having two kinds of motion. One is in the upward direction and the other is in the forward direction. The vertically upward motion can be considered as the motion in the y-axis. This will be the vertical component of the vector. While going upstairs you will be moving horizontally forwards which is considered as in x-axis. Thus your horizontal motion will be the horizontal component of actual motion. In short, we can say that our motion is resolved into two components. No more other components can be made in this 2D motion.
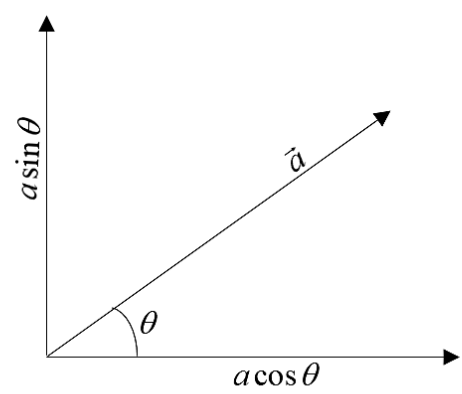
Therefore, the correct answer for the question has been obtained. it is given as option A.
Note:
The resultant of the vector will be the square root of the sum of squares of each of the components of a vector. Let the vector be given as
And the angle between the component and the resultant vector will be,
Complete step-by-step solution:
In a planar condition or a two-dimensional configuration, we will be moving either in a horizontal direction or vertical direction or both can also be possible. Let us assume a situation for example. Suppose you are going upstairs. When we move or go upstairs we will be having two kinds of motion. One is in the upward direction and the other is in the forward direction. The vertically upward motion can be considered as the motion in the y-axis. This will be the vertical component of the vector. While going upstairs you will be moving horizontally forwards which is considered as in x-axis. Thus your horizontal motion will be the horizontal component of actual motion. In short, we can say that our motion is resolved into two components. No more other components can be made in this 2D motion.

Therefore, the correct answer for the question has been obtained. it is given as option A.
Note:

The resultant of the vector will be the square root of the sum of squares of each of the components of a vector. Let the vector be given as
And the angle between the component and the resultant vector will be,
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




