Question

The measure of one angle of a parallelogram is \[{{80}^{\circ }}\]. What is the measure of the remaining angles?

Answer 1

Hint: We know that a parallelogram is a quadrilateral with opposite sides parallel, so we can say the opposite angles are also parallel, that is a parallelogram consisting of two pairs with the same angle. Now, consider x to be the angle \[\angle A\] of the parallelogram, then by using the property of parallelogram to determine the answer.

Complete step by step solution:
For clear understanding the concept of parallelogram figure is given below:
                       

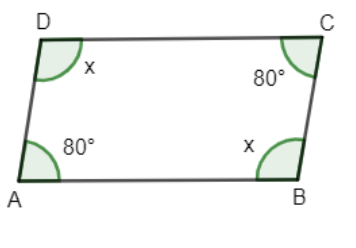
Above Figure is shown as a parallelogram which is also quadrilateral.
We know that the sum of adjacent angles of a parallelogram \[={{180}^{\circ }}\].
Consider x be the one angle of the parallelogram
As we know that \[\angle A={{80}^{\circ }}\] and also by knowing that sum of adjacent angles of a parallelogram is \[{{180}^{\circ }}\] therefore, we get:
\[\angle A+\angle B={{180}^{\circ }}\]
By substituting the value of \[\angle A={{80}^{\circ }}\] in above equation we get:
\[{{80}^{\circ }}+\angle B={{180}^{\circ }}\]
By simplifying this we get:
\[\angle B={{180}^{\circ }}-{{80}^{\circ }}\]
By Further solving this we get:
\[\angle B={{100}^{\circ }}\]
Now since it is a parallelogram the opposite angles will be equal to them
That means
\[\angle A=\angle C\]
But as we know that \[\angle A={{80}^{\circ }}\] therefore, \[\angle C={{80}^{\circ }}\]
Now, we can know that opposite angles are equal in parallelogram that means
\[\angle B=\angle D\]
As we know that \[\angle B={{100}^{\circ }}\] therefore, \[\angle D={{100}^{\circ }}\]
Hence, we get the angles are \[\angle A={{80}^{\circ }}\], \[\angle B={{100}^{\circ }}\],\[\angle C={{80}^{\circ }}\], \[\angle D={{100}^{\circ }}\]
Therefore, all the angles of parallelogram are \[{{80}^{\circ }},{{100}^{\circ }},{{80}^{\circ }},{{100}^{\circ }}\].
So, the correct answer is “Option B”.

Note: We can also find it in a simple way, it is given the one angle that is \[{{80}^{\circ }}\] and the same as considering x is there for another angle. And also the sum of the angle of the quadrilateral is \[{{360}^{\circ }}\]. We will get: \[x+x+{{80}^{\circ }}+{{80}^{\circ }}={{360}^{\circ }}\]. Therefore, by simplifying this we get: \[2x={{360}^{\circ }}-{{160}^{\circ }}\] and by further solving this \[2x={{200}^{\circ }}\] from this we can find the value of x that is \[x={{100}^{\circ }}\] As you can see here, we have got the same answer as we get in the solution from alternative method.