Question

The measure of two consecutive angles in a parallelogram are in the ratio $5:4$. What is the measure of an obtuse angle of the parallelogram?

Answer 1

Hint: We know that the sum of two adjacent angles in a parallelogram is ${180^ \circ }$. So, with the help of this property, we can find these two angles as the ratio of these two angles is given in the question. We also know that the obtuse angle is that angle which is greater than $90$ degrees and the angle which is a multiple of five in this question is the greater angle and supposed to be the obtuse angle.

Complete step by step answer:

.
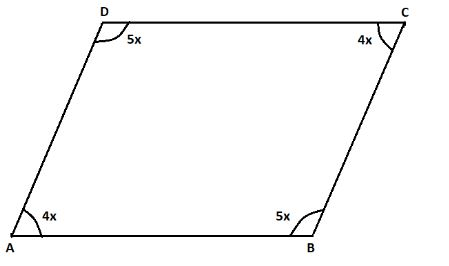
In the above question, it is given that we have a parallelogram in which the ratio of its consecutive angles is given as $5:4$.Let the value of $\angle A$ is $4x$.Therefore, the value of $\angle B$ will be $5x$. We know that the sum of consecutive angles in a parallelogram is $180$ degrees.Therefore,
$ \Rightarrow 4x + 5x = 180$
$ \Rightarrow 9x = 180$
On cross-multiplication, we get
$ \Rightarrow x = \dfrac{{180}}{9}$
On division, we get
$ \Rightarrow x = 20$
Now, $\angle A = 4x = 4 \times 20 = 80$
$\therefore \angle B = 5x = 5 \times 20 = 100$

Therefore, $\angle A$ has a measure of less than $90$ degrees and $\angle B$ has a measure of greater than $90$ degrees. So $\angle B$ is the obtuse angle and has a measure of $100$ degrees.

Note: We can also do this question by adding all the angles and putting their sum up to $360$ degrees. The properties of a parallelogram are as follows: The opposite sides are parallel and equal. The opposite angles are equal. The consecutive angles are supplementary.If any of the angles is a right angle, then all the other angles will be the right angle. The two diagonals bisect each other.