Question

The minimum distance of the center of the ellipse \[\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1\] from the chord of contact of mutually perpendicular tangents of the ellipse is
(A) \[\dfrac{144}{5}\]
(B) \[\dfrac{16}{5}\]
(C) \[\dfrac{9}{5}\]
(D) None of these

Answer 1

Hint: he equation of the ellipse is, \[\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1\] . We know the general equation of an ellipse, \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] . Now, compare \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] and \[\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1\] , and get the value of \[{{a}^{2}}\] and \[{{b}^{2}}\] . We know that the perpendicular tangents meet at a point on the director circle. We know the equation of the director circle, \[{{x}^{2}}+{{y}^{2}}=\sqrt{{{a}^{2}}+{{b}^{2}}}\] . Now, get the equation of the director circle. The coordinates of the general point on the director circle \[\left( 5\cos \theta ,5\sin \theta \right)\] . We know the standard equation of chord of contact with respect to \[\left( {{x}_{1}},{{y}_{1}} \right)\] of ellipse is, \[\dfrac{x{{x}_{1}}}{{{a}^{2}}}+\dfrac{y{{y}_{1}}}{{{b}^{2}}}=1\] . Use this and get the equation of the chord of the contact with respect to the point \[\left( 5\cos \theta ,5\sin \theta \right)\] . The center of the ellipse is \[\left( 0,0 \right)\] and the chord of the contact \[\dfrac{x\left( 5\cos \theta \right)}{16}+\dfrac{y\left( 5\sin \theta \right)}{9}-1=0\] . We know the formula of the distance of the point \[\left( {{x}_{1}},{{y}_{1}} \right)\] from the equation of the line \[ax+by+c\] , \[\text{Distance}=\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\] . Use this formula and get the distance of the center of the ellipse and the chord of the contact. Now, put \[{{\cos }^{2}}\theta =0\] and get the minimum value of the distance.

Complete step-by-step solution:
According to the question, it is given that we have an ellipse, \[\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1\] and we have to find the minimum distance of the center of the ellipse \[\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1\] from the chord of contact of mutually perpendicular tangents of the ellipse.
The equation of the ellipse = \[\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1\] ……………….(1)
The center of the ellipse \[\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1\] is at the origin.
The coordinates of the center of the ellipse = \[\left( 0,0 \right)\] ………......…………….(2)
The perpendicular tangents of the ellipse meet at the point which lies on the director circle.

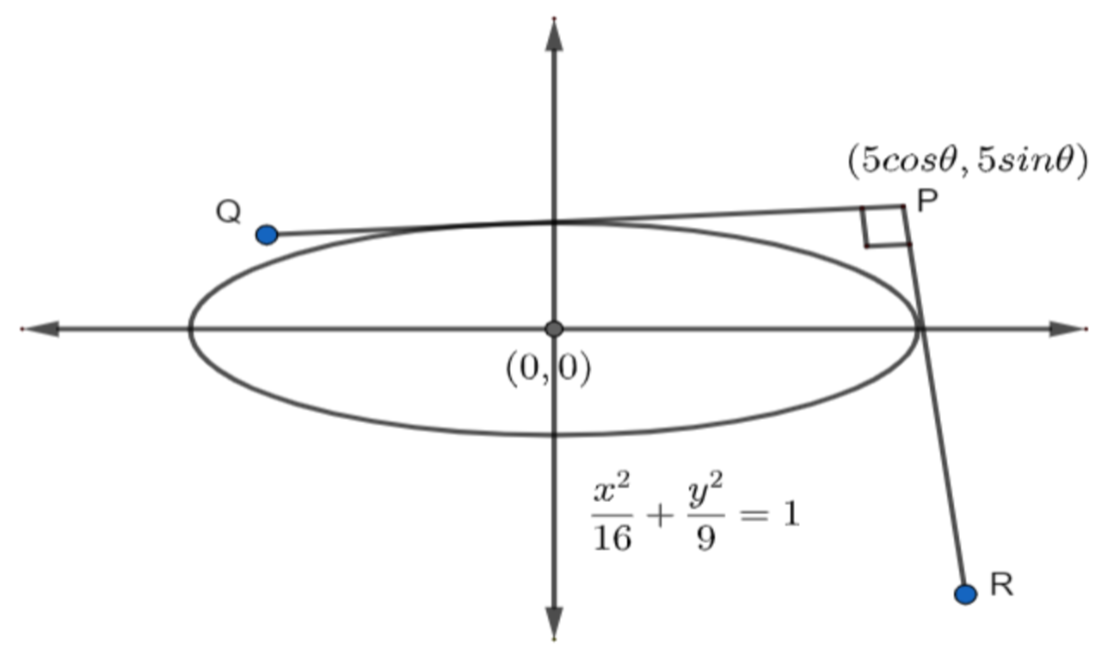
We know the standard equation of an ellipse, \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] ……………………………………..(3)
On comparing equation (1) and equation (3), we get
\[{{a}^{2}}=16\] ……………………………………………(4)
\[{{b}^{2}}=9\] ……………………………………………(5)
We know that the perpendicular tangents meet at the point on the director circle,
The standard equation of the director circle,
\[{{x}^{2}}+{{y}^{2}}=\sqrt{{{a}^{2}}+{{b}^{2}}}\] ………………………………………….(6)
Now, from equation (4), equation (5), and equation (6), we get
\[\begin{align}
  & \Rightarrow {{x}^{2}}+{{y}^{2}}=\sqrt{16+9} \\
 & \Rightarrow {{x}^{2}}+{{y}^{2}}=\sqrt{25} \\
\end{align}\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}=5\] …………………………………..……(7)
The coordinates of the general point on the director circle \[\left( 5\cos \theta, 5\sin \theta \right)\] ………………………………………(8)
We know the standard equation of chord of contact with respect to \[\left( {{x}_{1}},{{y}_{1}} \right)\] of ellipse is,
\[\dfrac{x{{x}_{1}}}{{{a}^{2}}}+\dfrac{y{{y}_{1}}}{{{b}^{2}}}=1\] …………………………………………..(9)
From equation (1), equation (8), and equation (9), we get
\[\Rightarrow \dfrac{x\left( 5\cos \theta \right)}{16}+\dfrac{y\left( 5\sin \theta \right)}{9}=1\]
\[\Rightarrow \dfrac{x\left( 5\cos \theta \right)}{16}+\dfrac{y\left( 5\sin \theta \right)}{9}-1=0\] …………………………………………(10)
We know the formula of the distance of the point \[\left( {{x}_{1}},{{y}_{1}} \right)\] from the equation of the line \[ax+by+c\] , \[\text{Distance}=\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\] ………………………………………….(11)
From equation (2), we have the coordinates of the center.
Using the formula shown in equation (11) to get the distance of the center of the ellipse from the line \[\dfrac{x\left( 5\cos \theta \right)}{16}+\dfrac{y\left( 5\sin \theta \right)}{9}-1=0\] .
Now, from equation (2), equation (10), and equation (11), we get
The distance of the point \[\left( 0,0 \right)\] from the equation of the chord of contact \[\dfrac{x\left( 5\cos \theta \right)}{16}+\dfrac{y\left( 5\sin \theta \right)}{9}-1=0\],
Distance \[=\dfrac{\left| \left( \dfrac{0\left( 5\cos \theta \right)}{16}+\dfrac{0\left( 5\sin \theta \right)}{9}-1 \right) \right|}{\sqrt{{{\left( \dfrac{5\cos \theta }{16} \right)}^{2}}+{{\left( \dfrac{5\sin \theta }{9} \right)}^{2}}}}\]
\[=\dfrac{\left| \left( -1 \right) \right|}{\sqrt{{{\left( \dfrac{5\cos \theta }{16} \right)}^{2}}+{{\left( \dfrac{5\sin \theta }{9} \right)}^{2}}}}\]
\[=\dfrac{1}{\sqrt{\dfrac{25{{\cos }^{2}}\theta }{256}+\dfrac{25{{\sin }^{2}}\theta }{81}}}\] ……………………………………………..(12)
We know the identity, \[{{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1\] ……………………………………………(13)
Now, simplifying equation (13), we get
\[\Rightarrow {{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1\]
\[\Rightarrow {{\sin }^{2}}\theta =1-{{\cos }^{2}}\theta \] ………………………………………(14)
From equation (12) and equation (14), we get
Distance \[=\dfrac{1}{\sqrt{\dfrac{25{{\cos }^{2}}\theta }{256}+\dfrac{25\left( 1-{{\cos }^{2}}\theta \right)}{81}}}\]
Distance \[=\dfrac{1}{\sqrt{\dfrac{25{{\cos }^{2}}\theta }{256}+\dfrac{25}{81}-\dfrac{25{{\cos }^{2}}\theta }{81}}}\]
Distance \[=\dfrac{1}{\sqrt{{{\cos }^{2}}\theta \left( \dfrac{25}{256}-\dfrac{25}{81} \right)+\dfrac{25}{81}}}\] …………………………………………....(15)
The general distance of the center of the ellipse from the chord of contact of mutually perpendicular tangents of the ellipse = \[\dfrac{1}{\sqrt{{{\cos }^{2}}\theta \left( \dfrac{25}{256}-\dfrac{25}{81} \right)+\dfrac{25}{81}}}\] …………………………………………(16)
We have to find the minimum distance of the center of the ellipse \[\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1\] from the chord of contact of mutually perpendicular tangents of the ellipse.
It means that when the denominator of \[\dfrac{1}{\sqrt{{{\cos }^{2}}\theta \left( \dfrac{25}{256}-\dfrac{25}{81} \right)+\dfrac{25}{81}}}\] is maximum then the distance will be minimum And the denominator will be maximum when \[{{\cos }^{2}}\theta \] is equal to 0.
Now, on putting \[{{\cos }^{2}}\theta =0\] in equation (16), we get
The general distance of the center of the ellipse from the chord of contact of mutually perpendicular tangents of the ellipse,
\[\begin{align}
  & =\dfrac{1}{\sqrt{0\left( \dfrac{25}{256}-\dfrac{25}{81} \right)+\dfrac{25}{81}}} \\
 & =\dfrac{1}{\sqrt{\dfrac{25}{81}}} \\
 & =\dfrac{9}{5} \\
\end{align}\]
Therefore, the general distance of the center of the ellipse from the chord of contact of mutually perpendicular tangents of the ellipse is \[\dfrac{9}{5}\] .
Hence the correct option is (C).

Note: In this question, one might do a silly mistake while figuring out the minimum value of \[\dfrac{1}{\sqrt{{{\cos }^{2}}\theta \left( \dfrac{25}{256}-\dfrac{25}{81} \right)+\dfrac{25}{81}}}\] . Here, one might think that by putting \[{{\cos }^{2}}\theta =1\] in \[\dfrac{1}{\sqrt{{{\cos }^{2}}\theta \left( \dfrac{25}{256}-\dfrac{25}{81} \right)+\dfrac{25}{81}}}\] , we can get its minimum value. This is wrong because putting the value of \[{{\cos }^{2}}\theta \] equal to 1 will not give the minimum value of \[\dfrac{1}{\sqrt{{{\cos }^{2}}\theta \left( \dfrac{25}{256}-\dfrac{25}{81} \right)+\dfrac{25}{81}}}\] . In the denominator we have the term \[{{\cos }^{2}}\theta \left( \dfrac{25}{256}-\dfrac{25}{81} \right)\] which is negative. So, to make the denominator maximum we must reduce the negative term. So, on putting \[{{\cos }^{2}}\theta =0\] , we get the negative term equal to zero which makes the denominator to reach its maximum value.